题目内容

10．在数列{an}中，前n项和为Sn，${a_n}=（3n-19）•{e^n}$，则当Sn最小时，n的值为（　　）
A．5B．6C．7D．8

分析 由数列前n项和的性质可知：3当n-19≤0，即n≤6，则an≤0，因此当n=6时，Sn最小．

解答 解：令an≤0，即3n-19≤0，则n≤6，
故当1≤n≤6时，an＜0；
当n≥7时，an＞0，
故当n=6时，Sn最小．
故选B．

点评 本题考查数列的性质，考查数列与不等式的应用，考查计算能力，属于基础题．

练习册系列答案
相关题目
20．复数$z=\frac{-2+2i}{1+i}$的共轭复数是（　　）
A．1+iB．1-iC．2iD．-2i
1．已知α∈（0，π），若sinα+cosα=$\frac{\sqrt{3}}{3}$，则cos2α-sin2α=（　　）
A．-$\frac{\sqrt{5}}{3}$B．-$\frac{\sqrt{2}}{3}$C．$\frac{\sqrt{5}}{3}$D．$\frac{\sqrt{2}}{3}$
18．${∫}_{-1}^{1}$（$\sqrt{1-{x}^{2}}$+xcosx）dx=$\frac{π}{2}$．
5．已知x2+y2-4x-2y-4=0，则$\frac{2x+3y+1}{x+2}$的最小值是（　　）
A．-2B．$-\frac{17}{4}$C．$-\frac{29}{5}$D．$2-\frac{{9\sqrt{7}}}{7}$
15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），且|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2$\sqrt{3}$，则$\overrightarrow{a}$与$\overrightarrow{b}$ 的夹角为$\frac{π}{6}$．
2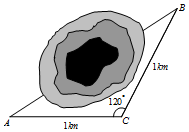．如图，在高速公路建设中需要确定隧道的长度，工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km，且∠ACB=120°，则A、B两点间的距离为（　　）
A．$\sqrt{3}$kmB．$\sqrt{2}$kmC．1.5kmD．2km
19．函数f（x）=x3-3x2-9x+1的单调递减区间为（　　）
A．（-1，3）B．（-∞，-1）或（3，+∞）C．（-3，1）D．（-∞，-3）或（1，+∞）
20．设{an}是首项大于零的等比数列，则“a12＜a22”是“数列{an}为递增数列”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网