题目内容
5.已知b>a>0,则M=$\frac{{a}^{2}+2ab+{b}^{2}}{ab-{a}^{2}}$的最小值是8.分析 化简M=$\frac{1+2\frac{b}{a}+(\frac{b}{a})^{2}}{\frac{b}{a}-1}$,从而令$\frac{b}{a}$=t,t>1;从而化简M=$\frac{{t}^{2}+2t+1}{t-1}$=(t-1)+$\frac{4}{t-1}$+4,利用基本不等式求最小值.
解答 解:M=$\frac{{a}^{2}+2ab+{b}^{2}}{ab-{a}^{2}}$=$\frac{1+2\frac{b}{a}+(\frac{b}{a})^{2}}{\frac{b}{a}-1}$,
令$\frac{b}{a}$=t,由b>a>0知t>1;
故M=$\frac{{t}^{2}+2t+1}{t-1}$=(t-1)+$\frac{4}{t-1}$+4≥8,
(当且仅当t-1=$\frac{4}{t-1}$,即t=3时,等号成立);
故答案为:8.
点评 本题考查了学生的化简能力及基本不等式的应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.设集合P={x|x>1},Q={x|x>0},则下列结论正确的是( )
| A. | P?Q | B. | Q?P | C. | P=Q | D. | P∪Q=R |
16.阅读如图的程序框图,运行相应的程序,若$f(x)=cos\frac{π}{3}x$,则输出的S的值为( )
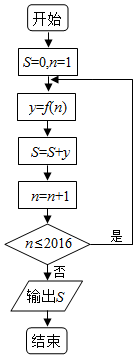

| A. | 0 | B. | 671.5 | C. | 671 | D. | 672 |
13.已知函数f(x)=cos2x-sin2x,下列说法错误的是( )
| A. | f(x)的最小正周期为π | B. | x=$\frac{π}{2}$是f(x)的一条对称轴 | ||
| C. | f(x)在(-$\frac{π}{4}$,$\frac{π}{4}$)上单调递增 | D. | |f(x)|的值域是[0,1] |
17.分段函数f(x)=$\left\{\begin{array}{l}{a\sqrt{x}+b,x≥1}\\{xcos\frac{π}{2}x,x<1}\end{array}\right.$在x=1处可导,则( )
| A. | a=0,b=-1 | B. | a=2,b=1 | C. | a=-π,b=π | D. | a=0,b=0 |
14.若集合M={x|log2(x-1)<-1},N={x|$\frac{1}{4}$≤($\frac{1}{2}$)x+1<1},则∁R(M∪N)=( )
| A. | {x|-1<x<2} | B. | {x|x≤-1或x$≥\frac{3}{2}$} | C. | {x|0<x<$\frac{3}{2}$} | D. | {x|x≤0或x≥2} |