题目内容
17.分段函数f(x)=$\left\{\begin{array}{l}{a\sqrt{x}+b,x≥1}\\{xcos\frac{π}{2}x,x<1}\end{array}\right.$在x=1处可导,则( )| A. | a=0,b=-1 | B. | a=2,b=1 | C. | a=-π,b=π | D. | a=0,b=0 |
分析 由函数在x=1处可导,可知在x=1处连续,由分段函数求出x=1时的左右导数得答案.
解答 解:分段函数f(x)=$\left\{\begin{array}{l}{a\sqrt{x}+b,x≥1}\\{xcos\frac{π}{2}x,x<1}\end{array}\right.$在x=1处可导,则必连续,
则f(1)=a+b=0,
又$\underset{lim}{x→{1}^{-}}xcos\frac{π}{2}x=0$,f′(1+)=$\frac{a}{2}$,
∴a=b=0.
故选:D.
点评 本题考查函数连续与可导的关系,是基础的计算题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
8.若直线l被圆C:x2+y2=2所截的弦长不小于2,下列方程表示的曲线中与直线l一定有公共点的是( )
| A. | y=x2 | B. | (x-1)2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{2}+{y^2}=1$ |
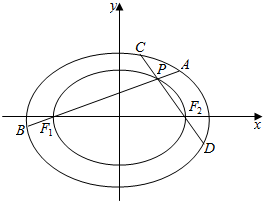 如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.
如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.