题目内容
14．若集合M={x|log2（x-1）＜-1}，N={x|$\frac{1}{4}$≤（$\frac{1}{2}$）x+1＜1}，则∁R（M∪N）=（ ）| A． | {x|-1＜x＜2} | B． | {x|x≤-1或x$≥\frac{3}{2}$} | C． | {x|0＜x＜$\frac{3}{2}$} | D． | {x|x≤0或x≥2} |
分析 由对数运算及指数运算可知M=（1，$\frac{3}{2}$），N=（-1，1]，从而求M∪N=（-1，$\frac{3}{2}$）及∁R（M∪N）={x|x≤-1或x$≥\frac{3}{2}$}．
解答 解：∵log2（x-1）＜-1，
∴0＜x-1＜$\frac{1}{2}$，
故M=（1，$\frac{3}{2}$），
∵$\frac{1}{4}$≤（$\frac{1}{2}$）x+1＜1，
∴0＜x+1≤2，
∴N=（-1，1]，
故M∪N=（-1，$\frac{3}{2}$），
故∁R（M∪N）={x|x≤-1或x$≥\frac{3}{2}$}，
故选：B．
点评 本题考查了对数运算及指数运算的应用，同时考查了集合的化简与集合的运算．
练习册系列答案
相关题目
4．设m＜0，点M（m，-2m）为角α的终边上一点，则$\frac{1}{{2sinαcosα+{{cos}^2}α}}$的值为（ ）
| A． | $-\frac{5}{3}$ | B． | -2 | C． | $\frac{2}{3}$ | D． | $\frac{10}{3}$ |
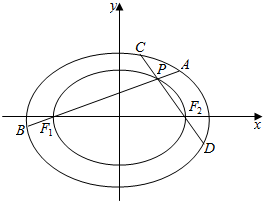如图，已知点F1，F2是椭圆C1：$\frac{{x}^{2}}{2}$+y2=1的两个焦点，椭圆C2：$\frac{{x}^{2}}{2}$+y2=λ经过点F1，F2，点P是椭圆C2上异于F1，F2的任意一点，直线PF1和PF2与椭圆C1的交点分别是A，B和C，D，设AB、CD的斜率为k，k′．