题目内容
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽AB为2米,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为O,对称轴与地面垂直,沟深2米,沟中水深1米.
(Ⅰ)求水面宽;
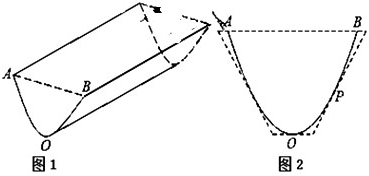
(Ⅱ)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
(Ⅲ)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
(Ⅰ)求水面宽;
(Ⅱ)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
(Ⅲ)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?

考点:棱柱、棱锥、棱台的体积,抛物线的应用
专题:综合题,导数的综合应用,空间位置关系与距离
分析:(Ⅰ)建立适当直角坐标系,设抛物线方程为y=ax2(-1≤x≤1),由抛物线过点B(1,2),可得a=2,可求出抛物线方程,从而求出水面宽;(Ⅱ)利用定积分求出曲面的面积,再利用柱体的体积公式求出体积;
(Ⅲ)易知为使挖掉的土最少,等腰梯形的两腰必须同抛物线相切,设切点P(t,2t2)(0<t≤1)是抛物线弧OB上的一点,过P作抛物线的切线得到如上图所示的直角梯形OCDE,则切线CD的方程为:y-2t2=4t(x-t),于是C(
t,0),D(
t+
,2),记梯形OCDE的面积为S,则S=2((
t+
t+
)×2×
=2(t+
),利用基本不等式即可得出结论.
(Ⅲ)易知为使挖掉的土最少,等腰梯形的两腰必须同抛物线相切,设切点P(t,2t2)(0<t≤1)是抛物线弧OB上的一点,过P作抛物线的切线得到如上图所示的直角梯形OCDE,则切线CD的方程为:y-2t2=4t(x-t),于是C(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2t |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2t |
| 1 |
| 2 |
| 1 |
| 2t |
解答:
 解:(Ⅰ)如图建立直角坐标系,
解:(Ⅰ)如图建立直角坐标系,
设抛物线方程为y=ax2(-1≤x≤1).
则由抛物线过点B(1,2),可得a=2.
于是抛物线方程为y=2x2(-1≤x≤1).
当y=1时,x=±
,由此知水面宽为
(米).
(Ⅱ)V=2×150
(1-2x2)dx=100
(立方米)
(Ⅲ)为使挖掉的土最少,等腰梯形的两腰必须同抛物线相切.
设切点P(t,2t2)(0<t≤1)是抛物线弧OB上的一点,过P作抛物线的切线得到如上图所示的直角梯形OCDE,则切线CD的方程为:y-2t2=4t(x-t),于是C(
t,0),D(
t+
,2).
记梯形OCDE的面积为
S,则S=2(
t+
t+
)×2×
=2(t+
)≥2
,
当且仅当t=
,t=
时,等号成立,所以改挖后的沟底宽为
米时,所挖的土最少.
 解:(Ⅰ)如图建立直角坐标系,
解:(Ⅰ)如图建立直角坐标系,设抛物线方程为y=ax2(-1≤x≤1).
则由抛物线过点B(1,2),可得a=2.
于是抛物线方程为y=2x2(-1≤x≤1).
当y=1时,x=±
| ||
| 2 |
| 2 |
(Ⅱ)V=2×150
| ∫ |
0 |
| 2 |
(Ⅲ)为使挖掉的土最少,等腰梯形的两腰必须同抛物线相切.
设切点P(t,2t2)(0<t≤1)是抛物线弧OB上的一点,过P作抛物线的切线得到如上图所示的直角梯形OCDE,则切线CD的方程为:y-2t2=4t(x-t),于是C(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2t |
记梯形OCDE的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2t |
| 1 |
| 2 |
| 1 |
| 2t |
| 2 |
当且仅当t=
| 1 |
| 2t |
| ||
| 2 |
| ||
| 2 |
点评:本题考查抛物线的标准方程、定积分的应用、基本不等式在求函数的最值中的应用,考查学生分析解决问题的能力,知识综合性强.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
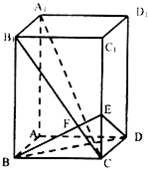 已知长方体AC1中,棱AB=BC=1,棱BB1=2,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
已知长方体AC1中,棱AB=BC=1,棱BB1=2,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.