题目内容
已知PA、PB、PC是三棱锥P-ABC的三条棱,PA=PB=PC,且PA,PB,PC夹角都是60°,那么直线PC与平面PAB所成角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:由已知得三棱锥P-ABC是正四面体,设这个正四面体的棱长为2,作PO⊥平面ABC,交ABC于点O,以O为原点,建立空间直角坐标系O-xyz,利用向量法能求出直线PC与平面PAB所成角的余弦值.
解答:
解: ∵PA、PB、PC是三棱锥P-ABC的三条棱,
∵PA、PB、PC是三棱锥P-ABC的三条棱,
PA=PB=PC,且PA,PB,PC夹角都是60°,
∴三棱锥P-ABC是正四面体,
设这个正四面体的棱长为2,作PO⊥平面ABC,交ABC于点O,
则PO=
=
,
以O为原点,建立如图所示的空间直角坐标系O-xyz,
则P(0,0,
),C(-1,
,0),
A(0,-
,0),B(1,
,0),
=(-1,
,-
),
=(0,-
,-
),
=(1,
,-
),
设平面PAB的法向量为
=(x,y,z),
则
,取z=1,得
=(
,-
,1),
设直线PC与平面PAB所成角为θ,
sinθ=|cos<
,
>|=
=
=
.
∴cosθ=
=
.
∴直线PC与平面PAB所成角的余弦值是
.
故选:D.
 ∵PA、PB、PC是三棱锥P-ABC的三条棱,
∵PA、PB、PC是三棱锥P-ABC的三条棱,PA=PB=PC,且PA,PB,PC夹角都是60°,
∴三棱锥P-ABC是正四面体,
设这个正四面体的棱长为2,作PO⊥平面ABC,交ABC于点O,
则PO=
(
|
2
| ||
| 3 |
以O为原点,建立如图所示的空间直角坐标系O-xyz,
则P(0,0,
2
| ||
| 3 |
| ||
| 3 |
A(0,-
2
| ||
| 3 |
| ||
| 3 |
| PC |
| ||
| 3 |
2
| ||
| 3 |
| PA |
2
| ||
| 3 |
2
| ||
| 3 |
| PB |
| ||
| 3 |
2
| ||
| 3 |
设平面PAB的法向量为
| n |
则
|
| n |
| 6 |
| 2 |
设直线PC与平面PAB所成角为θ,
sinθ=|cos<
| PC |
| n |
|
| ||||
|
|
2
| ||
| 2×3 |
| ||
| 3 |
∴cosθ=
1-(
|
| ||
| 3 |
∴直线PC与平面PAB所成角的余弦值是
| ||
| 3 |
故选:D.
点评:本题考查线面平行,线面垂直的性质的应用,考查线面所成角的求法,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
△ABC的外接圆的圆心为O,若
=
+
+
,则H是△ABC的( )
| OH |
| OA |
| OB |
| OC |
| A、外心 | B、内心 | C、重心 | D、垂心 |
已知函数y=f(x)对任意x∈R,恒有(f(x)-sinx)(f(x)-cosx)=0成立,则下列关于函数 y=f(x)的说法正确的是( )
| A、最小正周期是2π |
| B、值域是[-1,1] |
| C、是奇函数或是偶函数 |
| D、以上都不对 |
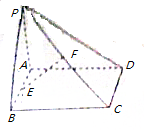 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.