题目内容
9.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地做了10次和 15次试验,并且利用最小二乘法,求得回归方程所对应的直线分别为l1:y=0.7x-0.5和l2:y=0.8x-1,则这两个人在试验中发现对变量x的观测数据的平均值S与对变量y的观测数据的平均值t的和是8.分析 由题意,两组数据变量x的观测值的平均值都是s,对变量y的观测值的平均值都是t,可得两组数据的样本中心点都是(s,t),数据的样本中心点一定在线性回归直线上,可知回归直线l1 和l2 都过点(s,t)两条直线有公共点(s,t),即两条直线的交点.即可得解.
解答 解:由题意,∵两组数据变量x的观测值的平均值都是s,对变量y的观测值的平均值都是t,
∴两组数据的样本中心点都是(s,t)
∵数据的样本中心点一定在线性回归直线上,
∴回归直线t1 和t2 都过点(s,t)
∴两条直线有公共点(s,t),
联立:$\left\{\begin{array}{l}{y=0.7x-0.5}\\{y=0.8x-1}\end{array}\right.$,
解得:s=5,t=3,
∴s+t=8.
故答案为:8
点评 本题考查线性回归方程的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知z=($\frac{1+i}{1-i}$)8,则$\overline{z}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
 如图,等腰三角形ABC中,E为底边BC的中点,△AEC沿AE折叠,将点C折到点P的位置,使二面角P-AE-B为60°,设点P在平面ABE上的射影为H.
如图,等腰三角形ABC中,E为底边BC的中点,△AEC沿AE折叠,将点C折到点P的位置,使二面角P-AE-B为60°,设点P在平面ABE上的射影为H.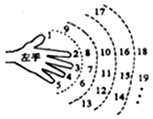 某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.
某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.