题目内容
17．已知集合M={-2，-1，0，1}，N={x|1≤2x≤4，x∈Z}，则M∩N=（ ）| A． | {-2，-1，0，1，2} | B． | {0，1} | C． | {-1，0，1} | D． | {-1，0，1，2} |
分析 求出N中不等式的解集，找出解集中的整数解确定出N，找出M与N的交集即可．
解答 解：由N中不等式变形得：20=1≤2x≤4=22，即0≤x≤2，x∈Z，
∴N={0，1，2}，
∵M={-2，-1，0，1}，
∴M∩N={0，1}，
故选：B．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
7．已知a＞0，a≠1，x＞0，则“a＞2”是“loga$\frac{x+1}{2}$≥$\frac{1}{2}$logax”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
8．已知命题p：存在x0＞0，使2${\;}^{{x}_{0}}$＜1，则￢p是（ ）
| A． | 对任意x＞0，都有2x≥1 | B． | 对任意x≤0，都有2x＜1 | ||
| C． | 存在x0＞0，使2${\;}^{{x}_{0}}$≥1 | D． | 存在x0≤0，使2${\;}^{{x}_{0}}$＜1 |
12．元宵节晚上有三支龙灯表演队，甲、乙两位志愿者各自参加其中一支表演队，每一位志愿者参加各支表演队的可能性相同，则这两位志愿者参加同一支表演队的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
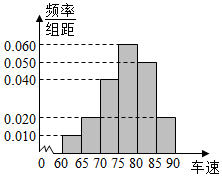2016年“双节”期间，高速公路车辆较多，某调查公司在一服务区从小型汽车中按进服务区的先后每间隔35辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段：