Question

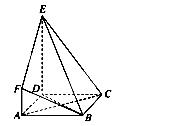
如图11-7，四棱锥P—ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E、F分别为CD、PB的中点。

（1）求证EF⊥平面PAB；

（2）设AB=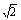BC，求AC与平面AEF所成的角的大小。

Answer 1

CD=ED，∴PE=BE，又F为PB中点，∴EF⊥PB ，又在Rt△PBC中，CF=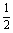PB，在Rt△PDB中，DF=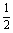PB，∴CF=DF，∴EF⊥CD，

又AB∥CD，∴EF⊥AB，∴EF⊥平面PAB；

（2）由已知PD⊥CD，PD⊥AD，又AD⊥CD，所以建立如图11-8所示的空间直角坐标系，设BC=a，