题目内容
函数f（x）的导函数为f′（x），对?x∈R，都有f′（x）＞f（x）成立，若f（ln2）=2，则不等式f（x）＞ex的解是（ ）
| A、x＞1 |
| B、0＜x＜1 |
| C、x＞ln2 |
| D、0＜x＜ln2 |
考点：利用导数研究函数的单调性
专题：
分析：造函数g（x）=
，利用导数可判断g（x）的单调性，再根据f（ln2）=2，求得g（ln2）=1，继而求出答案．
| f(x) |
| ex |
解答：
解：∵?x∈R，都有f′（x）＞f（x）成立，
∴f′（x）-f（x）＞0，于是有（
）′＞0，
令g（x）=
，则有g（x）在R上单调递增，
∵不等式f（x）＞ex，
∴g（x）＞1，
∵f（ln2）=2，
∴g（ln2）=1，
∴x＞ln2，
故选：C．
∴f′（x）-f（x）＞0，于是有（
| f(x) |
| ex |
令g（x）=
| f(x) |
| ex |
∵不等式f（x）＞ex，
∴g（x）＞1，
∵f（ln2）=2，
∴g（ln2）=1，
∴x＞ln2，
故选：C．
点评：本题考查导数的运算及利用导数研究函数的单调性，属中档题，解决本题的关键是根据选项及已知条件合理构造函数，利用导数判断函数的单调性．
练习册系列答案
阅读快车系列答案
相关题目
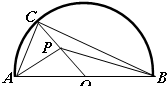如图，半圆的直径AB=6，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则（| PA |
| PB |
| PC |
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |