题目内容
7.已知实数变量x,y满足$\left\{\begin{array}{l}x+y≥1\\ x-y≥0\\ 2mx-y-2≤0\end{array}\right.$,且目标函数z=3x+y的最大值为8,则实数m的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
解答 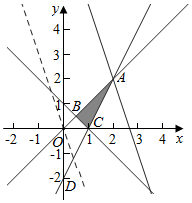 解:作出不等式对应的平面区域如图,
解:作出不等式对应的平面区域如图,
由选项知m>0,
由z=3x+y,得y=-3x+z,
平移直线y=-3x+z,由图象可知当直线y=-3x+z,经过点A时,直线y=-3x+z的截距最大,此时z最大为8,即3x+y=8
由$\left\{\begin{array}{l}{3x+y=8}\\{x-y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即A(2,2),
同时A也在2mx-y-2=0上,
∴4m-2-2=0,得m=1,
故选:D.
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划问题中的基本方法,要熟练掌握目标函数的几何意义.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.在等比数列{an}中,如果a1+a2=40,a3+a4=60,那么a5+a6等于( )
| A. | 80 | B. | 90 | C. | 95 | D. | 100 |
13.首项为-12的等差数列从第20项起开始为正数,则公差d满足( )
| A. | d>$\frac{12}{19}$ | B. | d<$\frac{2}{3}$ | C. | $\frac{12}{19}$≤d<$\frac{2}{3}$ | D. | $\frac{12}{19}$<d≤$\frac{2}{3}$ |
15.经过圆x2+y2+2y=0的圆心且与直线x+2y-2=0平行的直线方程是( )
| A. | x+2y-1=0 | B. | x+2y+2=0 | C. | x+2y+1=0 | D. | x+2y+3=0 |
12.已知等差数列{an}的前n项和为Sn,若2a5+3a7+2a9=14,则S13等于( )
| A. | 26 | B. | 28 | C. | 52 | D. | 13 |
16.在△ABC中,角A,B,C所对的边是a,b,c,已知a=2,则bcosC+ccosB等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 4 | D. | 2 |