题目内容
2.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点为F(3,0),且双曲线的渐进线与圆(x-3)2+y2=1相切,则该双曲线的标准方程为$\frac{{x}^{2}}{8}$-y2=1..分析 求出双曲线的渐近线方程,运用直线和圆相切的条件:d=r,可得c=3b=3,由a,b,c的关系可得a,进而得到所求双曲线的方程.
解答 解:由题意可得c=3,
双曲线的渐近线方程为y=±$\frac{b}{a}$x,
由双曲线的渐近线与圆(x-3)2+y2=1相切,
可得d=$\frac{3b}{\sqrt{{a}^{2}+{b}^{2}}}$=1,
可得3b=c=3,即b=1,
a=$\sqrt{{c}^{2}-{b}^{2}}$=2$\sqrt{2}$.
可得双曲线的方程为$\frac{{x}^{2}}{8}$-y2=1.
故答案为:$\frac{{x}^{2}}{8}$-y2=1.
点评 本题考查双曲线的方程的求法,注意运用渐近线方程和直线与圆相切的条件:d=r,考查运算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.已知数列{an}的前n项和Sn=1-3+5-7+…+(-1)n-1(2n-1)(n∈N*),则S17+S23+S50=( )
| A. | 90 | B. | 10 | C. | -10 | D. | 22 |
8.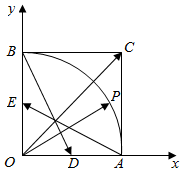 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )| A. | -$\sqrt{2}$ | B. | -2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{2}$ |
10.若命题p:0是偶数,命题q:2是3的约数,则下列命题中为真的是( )
| A. | p且q | B. | p或q | C. | 非p | D. | 以上都不对 |
17.已知向量$\vec a$,$\vec b$的夹角为60°,且$|{\vec a}|=2$,$|{\vec b}|=1$,当$|{\vec a-x\vec b}|$取得最小值时,实数x的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
7.已知实数变量x,y满足$\left\{\begin{array}{l}x+y≥1\\ x-y≥0\\ 2mx-y-2≤0\end{array}\right.$,且目标函数z=3x+y的最大值为8,则实数m的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |