题目内容
12.在等比数列{an}中,如果a1+a2=40,a3+a4=60,那么a5+a6等于( )| A. | 80 | B. | 90 | C. | 95 | D. | 100 |
分析 在等比数列{an}中,a1+a2,a3+a4,a5+a6构成等比数列,由此能求出结果.
解答 解:在等比数列{an}中,
∵a1+a2=40,a3+a4=60,a1+a2,a3+a4,a5+a6构成等比数列,
∴a5+a6=60×$\frac{60}{40}$=90.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
3.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得到如下频数分布表.
(1)作出这些数据的频率分布直方图(用阴影表示);
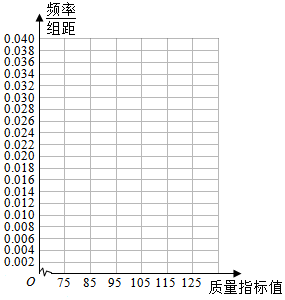
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计这种产品质量指标值的平均数$\overline{x}$及方差s2;
(3)当质量指标值位于(79.6,120.4)时,认为该产品为合格品.由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline{x}$,σ2近似为样本方差s2(每组数取中间值).
①利用该正态分布,求从该厂生产的产品中任取一件,该产品为合格品的概率;
②该企业每年生产这种产品10万件,生产一件合格品利润10元,生产一件不合格品亏损20元,则该企业的年利润是多少?
(提示:$\sqrt{104}$≈10.2,若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,P(μ-2σ<Z<μ+2σ)=0.9544)
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
| 频数 | 6 | 26 | x | 22 | 8 |

(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计这种产品质量指标值的平均数$\overline{x}$及方差s2;
(3)当质量指标值位于(79.6,120.4)时,认为该产品为合格品.由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline{x}$,σ2近似为样本方差s2(每组数取中间值).
①利用该正态分布,求从该厂生产的产品中任取一件,该产品为合格品的概率;
②该企业每年生产这种产品10万件,生产一件合格品利润10元,生产一件不合格品亏损20元,则该企业的年利润是多少?
(提示:$\sqrt{104}$≈10.2,若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,P(μ-2σ<Z<μ+2σ)=0.9544)
7.已知数列{an}的前n项和Sn=1-3+5-7+…+(-1)n-1(2n-1)(n∈N*),则S17+S23+S50=( )
| A. | 90 | B. | 10 | C. | -10 | D. | 22 |
17.如果实数x,y,满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$,则z=1-$\frac{2}{2x+3y}$的最大值为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | 0 | D. | $\frac{4}{7}$ |
4.已知集合A={-2,3},B={x|lnx>1},则A∩B=( )
| A. | {-2} | B. | {3} | C. | {-2,3} | D. | ∅ |
7.已知实数变量x,y满足$\left\{\begin{array}{l}x+y≥1\\ x-y≥0\\ 2mx-y-2≤0\end{array}\right.$,且目标函数z=3x+y的最大值为8,则实数m的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
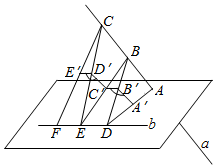 如图,直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A′,B′,C′,D′,E′分别为AD,DB,BE,EC,CF的中点.
如图,直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A′,B′,C′,D′,E′分别为AD,DB,BE,EC,CF的中点.