题目内容
17．在△ABC中，a，b，c分别是A，B，C的对边，且A=$\frac{2π}{3}$，b+2c=8，则当△ABC的面积取得最大值时，a的值为2$\sqrt{7}$．分析 由题意可得b=8-2c，代入三角形的面积公式S=$\frac{1}{2}$bcsin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$c（4-c），由基本不等式可得c和b值，由余弦定理可得a值．
解答 解：∵在△ABC中，A=$\frac{2π}{3}$，b+2c=8，
∴△ABC的面积S=$\frac{1}{2}$bcsin$\frac{2π}{3}$=$\frac{\sqrt{3}}{4}$bc=$\frac{\sqrt{3}}{4}$c（8-2c）
=$\frac{\sqrt{3}}{2}$c（4-c）≤$\frac{\sqrt{3}}{2}$（$\frac{c+4-c}{2}$）2=2$\sqrt{3}$，
当且仅当c=4-c即c=2时取等号，此时b=4，
由余弦定理可得a2=b2+c2-2bccosA=16+4-2×4×2×（-$\frac{1}{2}$）=28，
开方可得a=2$\sqrt{7}$，
故答案为：2$\sqrt{7}$．
点评 本题考查余弦定理的应用和三角形的面积计算公式，涉及基本不等式求最值，属中档题．
练习册系列答案
相关题目
7．已知实数变量x，y满足$\left\{\begin{array}{l}x+y≥1\\ x-y≥0\\ 2mx-y-2≤0\end{array}\right.$，且目标函数z=3x+y的最大值为8，则实数m的值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 1 |
5．
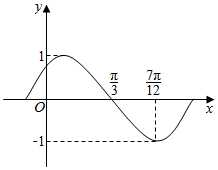将函数$y=sin（ωx+φ）（ω＞0，|φ|≤\frac{π}{2}）$的图象沿x轴方向向左平移$\frac{π}{3}$个单位，所得曲线的一部分图象如图，则ω，φ的值分别为（ ）
将函数$y=sin（ωx+φ）（ω＞0，|φ|≤\frac{π}{2}）$的图象沿x轴方向向左平移$\frac{π}{3}$个单位，所得曲线的一部分图象如图，则ω，φ的值分别为（ ）| A． | 1，$\frac{π}{3}$ | B． | 1，$-\frac{π}{3}$ | C． | 2，$\frac{π}{3}$ | D． | 2，$-\frac{π}{3}$ |
9．在平面直角坐标系中，双曲线C过点P（1，1），且其两条渐近线的方程分别为2x+y=0和2x-y=0，则双曲线C的标准方程为（ ）
| A． | $\frac{x^2}{3}-\frac{{4{y^2}}}{3}=1$ | B． | $\frac{{4{x^2}}}{3}-\frac{y^2}{3}=1$ | ||
| C． | $\frac{{4{x^2}}}{3}-\frac{y^2}{3}=1$或$\frac{x^2}{3}-\frac{{4{y^2}}}{3}=1$ | D． | $\frac{{4{y^2}}}{3}-\frac{x^2}{3}=1$ |
6．已知函数$f（x）=\left\{\begin{array}{l}x，|x|≤1\\ sin\frac{π}{2}x，|x|＞1\end{array}\right.$则下列结论正确的是（ ）
| A． | 函数f（x）在$[-\frac{π}{2}，\frac{π}{2}]$上单调递增 | B． | 函数f（x）的值域是[-1，1] | ||
| C． | ?x0∈R，f（-x0）≠-f（x0） | D． | ?x∈R，f（-x）≠f（x） |