题目内容
如图，三棱柱ABC-A1B2C3的底面是边长为4正三角形，AA1⊥平面ABC，AA1=2
，M为A1B1的中点．
（Ⅰ）求证：MC⊥AB；
（Ⅱ）在棱CC1上是否存在点P，使得MC⊥平面ABP？若存在，确定点P的位置；若不存在，说明理由．
（Ⅲ）若点P为CC1的中点，求二面角B-AP-C的余弦值．
| 6 |
（Ⅰ）求证：MC⊥AB；
（Ⅱ）在棱CC1上是否存在点P，使得MC⊥平面ABP？若存在，确定点P的位置；若不存在，说明理由．
（Ⅲ）若点P为CC1的中点，求二面角B-AP-C的余弦值．
考点：与二面角有关的立体几何综合题,直线与平面垂直的判定
专题：综合题,空间位置关系与距离,空间角
分析：（Ⅰ）取AB中点O，连接OM，OC，证明AB⊥平面OMC，可得MC⊥AB；
（Ⅱ）建立空间直角坐标系，设P（0，2
，t）（0≤t≤2
），要使直线MC⊥平面ABP，只要
•
=0，
•
=0，即可得出结论；
（Ⅲ）若点P为CC1的中点，求出平面PAC的一个法向量、平面PAB的一个法向量，利用向量的夹角公式，即可求二面角B-AP-C的余弦值．
（Ⅱ）建立空间直角坐标系，设P（0，2
| 3 |
| 6 |
| MC |
| OP |
| MC |
| AB |
（Ⅲ）若点P为CC1的中点，求出平面PAC的一个法向量、平面PAB的一个法向量，利用向量的夹角公式，即可求二面角B-AP-C的余弦值．
解答：
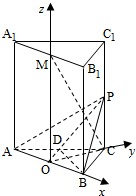（I）证明：取AB中点O，连接OM，OC．
∵M为A1B1中点，∴MO∥A1A，
又A1A⊥平面ABC，∴MO⊥平面ABC，
∴MO⊥AB
∵△ABC为正三角形，∴AB⊥CO
又MO∩CO=O，∴AB⊥平面OMC
又∵MC?平面OMC∴AB⊥MC
（II）解：以O为原点，建立空间直角坐标系．如图．
依题意O（0，0，0），A（-2，0，0）B（2，0，0），C（0，2
，0），M（0，0，2
）．
设P（0，2
，t）（0≤t≤2
），
则
=（0，2
，-2
），
=（4，0，0），
=（0，2
，t）．
要使直线MC⊥平面ABP，只要
•
=0，
•
=0，
即12-2
t=0，解得t=
．
∴P的坐标为（0，2
，
）．
∴当P为线段CC1的中点时，MC⊥平面ABP
（Ⅲ）解：取线段AC的中点D，则D（-1，
，0），易知DB⊥平面A1ACC1，
故
=（3，-
，0）为平面PAC的一个法向量．…．（11分）
又由（II）知
=（0，2
，-2
）为平面PAB的一个法向量．
设二面角B-AP-C的平面角为α，则cosα=|
|=
．
∴二面角B-AP-C 的余弦值为
．
（I）证明：取AB中点O，连接OM，OC．∵M为A1B1中点，∴MO∥A1A，
又A1A⊥平面ABC，∴MO⊥平面ABC，
∴MO⊥AB
∵△ABC为正三角形，∴AB⊥CO
又MO∩CO=O，∴AB⊥平面OMC
又∵MC?平面OMC∴AB⊥MC
（II）解：以O为原点，建立空间直角坐标系．如图．
依题意O（0，0，0），A（-2，0，0）B（2，0，0），C（0，2
| 3 |
| 6 |
设P（0，2
| 3 |
| 6 |
则
| MC |
| 3 |
| 6 |
| AB |
| OP |
| 3 |
要使直线MC⊥平面ABP，只要
| MC |
| OP |
| MC |
| AB |
即12-2
| 6 |
| 6 |
∴P的坐标为（0，2
| 3 |
| 6 |
∴当P为线段CC1的中点时，MC⊥平面ABP
（Ⅲ）解：取线段AC的中点D，则D（-1，
| 3 |
故
| DB |
| 3 |
又由（II）知
| MC |
| 3 |
| 6 |
设二面角B-AP-C的平面角为α，则cosα=|
| ||||
|
|
| ||
| 6 |
∴二面角B-AP-C 的余弦值为
| ||
| 6 |
点评：本小题主要考查空间直线与直线、直线与平面的位置关系、二面角等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查数形结合思想、化归与转化思想、函数与方程思想．
练习册系列答案
相关题目
在△ABC中，AD为BC边上的高，已知：AC=b；AB=c，AD=BC，求