Question

11．有两种规格的矩形钢板，甲型的宽度为a，乙型的宽度为2a，长度可以足够长，厚度不计，现把它们切割后拼接成一个角形钢板，焊缝为OM，记∠AOB=θ（0°＜θ＜180°）．
（1）若θ=135°，求tan∠AOM的值
（2）把OM的长度用θ表示，并求OM的最小值

Answer 1

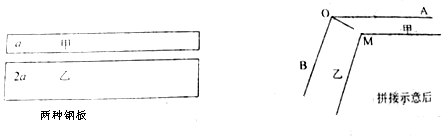
分析 （1）记∠AOM=x，∠BOM=135°-x，则$\frac{a}{sinx}=\frac{2a}{sin（135°-x）}$，即可求tan∠AOM的值
（2）自M点向边OA，OB作垂线，垂足分别为E，F，则O，M，E，F四点共圆，且OM为直径，求出EF，即可把OM的长度用θ表示，换元，利用基本不等式求OM的最小值．

解答 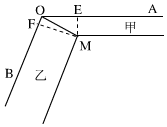解：（1）记∠AOM=x，∠BOM=135°-x，则$\frac{a}{sinx}=\frac{2a}{sin（135°-x）}$，
∴sin（135°-x）=2sinx，
化简可得tanx=$\frac{sin135°}{2+cos135°}$=$\frac{2\sqrt{2}+1}{7}$；
（2）自M点向边OA，OB作垂线，垂足分别为E，F，
则O，M，E，F四点共圆，且OM为直径，
EF=$\sqrt{{a}^{2}+4{a}^{2}-2a•2a•cos（180°-θ）}$=a$\sqrt{5+4cosθ}$，
由正弦定理得OM=$\frac{a\sqrt{5+4cosθ}}{sinθ}$．
令t=5+4cosθ（1＜t＜9），则OM=4a$\sqrt{\frac{t}{-{t}^{2}+10t-9}}$=4a$\sqrt{\frac{1}{-（t+\frac{9}{t}）+10}}$≥4a$\sqrt{\frac{1}{-6+10}}$=2a，
当t=3，即θ=120°时等号成立，故OM_min=2a．

点评 本题考查利用三角函数知识解决实际问题，考查直线定理的运用，考查基本不等式，属于中档题．