题目内容
3.已知等比数列{an}的公比q,前n项的和Sn,对任意的n∈N*,Sn>0恒成立,则公比q的取值范围是(-1,0)∪(0,+∞).分析 q≠1时,由Sn>0,知a1>0,从而$\frac{1-{q}^{n}}{1-q}$>0恒成立,由此利用分类讨论思想能求出公比q的取值范围.
解答 解:q≠1时,有Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,
∵Sn>0,∴a1>0,
则$\frac{1-{q}^{n}}{1-q}$>0恒成立,
①当q>1时,1-qn<0恒成立,即qn>1恒成立,由q>1,知qn>1成立;
②当q=1时,只要a1>0,Sn>0就一定成立;
③当q<1时,需1-qn>0恒成立,
当0<q<1时,1-qn>0恒成立,
当-1<q<0时,1-qn>0也恒成立,
当q<-1时,当n为偶数时,1-qn>0不成立,
当q=-1时,1-qn>0也不可能恒成立,
所以q的取值范围为(-1,0)∪(0,+∞).
故答案为:(-1,0)∪(0,+∞).
点评 本题考查等比数列的公比的取值范围的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
10.已知等比数列{an}满足a1=3,a2a3a4=54,则a3a4a8=( )
| A. | 162 | B. | ±162 | C. | 108 | D. | ±108 |
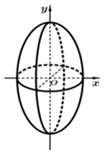 祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于$\frac{4}{3}π×{b^2}a$.
祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于$\frac{4}{3}π×{b^2}a$.