题目内容
已知等比数列{an}的各项均为正数,且a1+2a2=1,a32=4a2a6.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an,求数列{an•bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an,求数列{an•bn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)设数列{an}的公比为q,通过解方程组可求得a1与q,从而可求数列{an}的通项公式;
(Ⅱ)利用错位相减法可求得数列{an•bn}的前n项和Sn.
(Ⅱ)利用错位相减法可求得数列{an•bn}的前n项和Sn.
解答:
解:(Ⅰ)设数列{an}的公比为q,由
=4a2a6⇒
=4
,所以q2=
.
由条件可知q>0,故q=
.
由a1+2a2=1⇒a1+2a1•q=1⇒a1=
.
故数列{an}的通项公式为an=a1•qn-1=
.
(Ⅱ)bn=log2an=log2(
)n=-n,故an•bn=-n•(
)n
从而Sn=a1•b1+a2•b2+…+an-1•bn-1+an•bn=-[1•
+2•(
)2+…+(n-1)•(
)n-1+n•(
)n]
故
Sn=-[1•(
)2+2•(
)3+…+(n-1)•(
)n+n•(
)n+1]
两式相减得
Sn=-[
+(
)2+(
)3+…+(
)n-n•(
)n+1]=-
+n•(
)n+1=
•(
)n-
所以数列{an•bn}的前n项和Sn=(n+2)•(
)n-1.
| a | 2 3 |
| a | 2 3 |
| a | 2 4 |
| 1 |
| 4 |
由条件可知q>0,故q=
| 1 |
| 2 |
由a1+2a2=1⇒a1+2a1•q=1⇒a1=
| 1 |
| 2 |
故数列{an}的通项公式为an=a1•qn-1=
| 1 |
| 2n |
(Ⅱ)bn=log2an=log2(
| 1 |
| 2 |
| 1 |
| 2 |
从而Sn=a1•b1+a2•b2+…+an-1•bn-1+an•bn=-[1•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
两式相减得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
| n+2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以数列{an•bn}的前n项和Sn=(n+2)•(
| 1 |
| 2 |
点评:本题考查数列的求和,考查等比数列的通项公式与求和公式的综合应用,属于中档题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: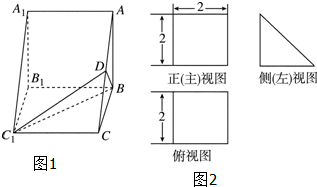 直三棱柱ABC-A1B1C1的直观图(图1)及三视图(图2)如图所示,D为AC的中点
直三棱柱ABC-A1B1C1的直观图(图1)及三视图(图2)如图所示,D为AC的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.