题目内容
已知不等式:mx2-(m+1)x+1<0
(1)当m=2时,求不等式的解集;
(2)当m>0时,解关于x的不等式.
(1)当m=2时,求不等式的解集;
(2)当m>0时,解关于x的不等式.
考点:一元二次不等式的解法
专题:分类讨论,不等式的解法及应用
分析:(1)m=2时,不等式为2x2-3x+1<0,解一元二次不等式即可;
(2)m>0时,不等式化为(mx-1)(x-1)<0,讨论
与1的大小,得出不等式的解集.
(2)m>0时,不等式化为(mx-1)(x-1)<0,讨论
| 1 |
| m |
解答:
解:(1)当m=2时,不等式为2x2-3x+1<0,
∴(2x-1)(x-1)<0;
解得
<x<1,
∴不等式的解集为{x|
<x<1};
(2)当m>0时,不等式可化为(mx-1)(x-1)<0,
即(x-
)(x-1)<0;
①若
>1,即0<m<1,则不等式的解集为{x|1<x<
};
②若
=1,即m=1,则不等式的解集为∅;
③若
<1,即m>1,则不等式的解集为{x|
<x<1}.
综上,0<m<1时,解集为{x|1<x<
},m=1时,解集为∅,m>1时,解集为{x|
<x<1}.
∴(2x-1)(x-1)<0;
解得
| 1 |
| 2 |
∴不等式的解集为{x|
| 1 |
| 2 |
(2)当m>0时,不等式可化为(mx-1)(x-1)<0,
即(x-
| 1 |
| m |
①若
| 1 |
| m |
| 1 |
| m |
②若
| 1 |
| m |
③若
| 1 |
| m |
| 1 |
| m |
综上,0<m<1时,解集为{x|1<x<
| 1 |
| m |
| 1 |
| m |
点评:本题考查了不等式的解法与应用问题,解题时应对字母系数进行分类讨论,是基础题目.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
设x,y是实数,则下列命题中是真命题的是( )
| A、若x<1,则x2<1 | ||||
| B、若lny2=0,则y=1 | ||||
| C、若sinx=siny,则x=y | ||||
D、若x<y,xy>0,则
|
 (文) 已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.
(文) 已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.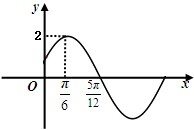 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<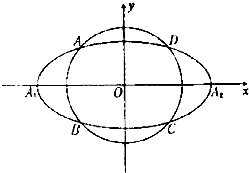 如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2:
如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2: