题目内容
已知函数y=
cos2x+
sinxcosx+1,x∈R,求:
(1)函数y的最大值;
(2)函数y的周期;
(3)函数y的单调增区间.
| 1 |
| 2 |
| ||
| 2 |
(1)函数y的最大值;
(2)函数y的周期;
(3)函数y的单调增区间.
考点:二倍角的余弦,两角和与差的正弦函数,三角函数的周期性及其求法,正弦函数的单调性
专题:三角函数的求值
分析:(1)由条件利用本题主要考查两角和的正弦公式,二倍角公式,化简函数的解析式为 y=
sin(2x+
)+
,可得函数的最大值.
(2)根据正弦函数的周期性,求得函数的周期.
(3)令2kπ-
≤2x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.
| 1 |
| 2 |
| π |
| 6 |
| 5 |
| 4 |
(2)根据正弦函数的周期性,求得函数的周期.
(3)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(1)函数y=
cos2x+
sinxcosx+1=
+
sin2x+1=
sin(2x+
)+
,
故函数的最大值为
+
=
.
(2)函数的周期为
=π.
(3)令2kπ-
≤2x+
≤2kπ+
,k∈z,求得kπ-
≤x≤kπ+
,
故函数的增区间为[kπ-
,kπ+
],k∈z.
| 1 |
| 2 |
| ||
| 2 |
| 1+cos2x |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 5 |
| 4 |
故函数的最大值为
| 1 |
| 2 |
| 5 |
| 4 |
| 7 |
| 4 |
(2)函数的周期为
| 2π |
| 2 |
(3)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
故函数的增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查两角和的正弦公式,二倍角公式,正弦函数的单调性和周期性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
已知P(-1,y)是角θ终边上一点,且sinθ=
,则y的值( )
2
| ||
| 5 |
| A、2 | B、-2 | C、±2 | D、1 |
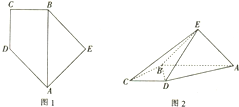 已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)
已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)