题目内容
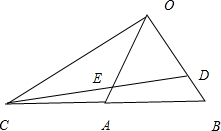
如图，已知在△OAB中，点C是以A为中心的点B的对称点，D是将
分成2：1的一个内分点，
和
交于点E，设
=
，
=
．
（1）用
，
表示
，
；
（2）若
=λ
，求实数λ的值．
| OB |
| DC |
| OA |
| OA |
| a |
| OB |
| b |
（1）用
| a |
| b |
| OC |
| DC |
（2）若
| OE |
| OA |
考点：平面向量的基本定理及其意义,平行向量与共线向量
专题：平面向量及应用
分析：（1）根据向量的几何意义计算即可，
（2）利用向量共线及向量相等的条件结合向量加法的三角形法则，可求λ的值
（2）利用向量共线及向量相等的条件结合向量加法的三角形法则，可求λ的值
解答：
解：（1）如图所示，∵设
=
，
=
，点C是以A为中心的点B的对称点，
∴
=
-
=
-2
=
-2(
-
)=2
-
=2
-
．
∵D是将
分成2：1的一个内分点，
∴
=
=
，
∴
=
-
=(2
-
)-
=2
-
，
（2）设
=μ
，
∵
=λ
又
=
-
=λ
-μ
=λ
-μ(
-2
)
=(λ-μ)
-
∵
=2
-
，
∴
解得λ=
| OA |
| a |
| OB |
| b |
∴
| OC |
| OB |
| CB |
| OB |
| AB |
| OB |
| OB |
| OA |
| OA |
| OB |
| a |
| b |
∵D是将
| OB |
∴
| OD |
| 2 |
| 3 |
| OB |
| 2 |
| 3 |
| b |
∴
| DC |
| OC |
| OD |
| a |
| b |
| 2 |
| 3 |
| b |
| a |
| 5 |
| 3 |
| b |
（2）设
| CE |
| CD |
∵
| OE |
| OA |
又
| OC |
| OE |
| CE |
| OA |
. |
| CD |
=λ
| a |
| 5 |
| 3 |
| b |
| a |
=(λ-μ)
| a |
| 5μ |
| 3 |
| b |
∵
| OC |
| a |
| b |
∴
|
解得λ=
| 4 |
| 5 |
点评：本题主要考查向量加法的三角形法则，向量共线\向量相等的条件，关键是要熟悉向量的各个知识点，会综合运用向量的知识解决问题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
为了帮助小型企业乙转型发展，大型国企甲将经营状况良好的某种消费品专卖批发店，以120万元的优惠价格转让给了企业乙，并约定从该店经营的利润中，首先保证所有职工每月工资开支10万元，再逐步偿还转让费（不计息），在国企甲提供的资料中显示：①这种消费品的进价为每件20元；②该店月销量Q（千件）与销售价格x（元）的关系如图所示；③每月需水电房租等各种开支22000元．