题目内容
2.求曲线f(x)=$\frac{x}{{{e^{2x}}}}$在x=2处的切线与x轴交点A的坐标.分析 求出函数的导数,可得曲线在x=2处切线的斜率,求得切点,运用点斜式方程,再由y=0,可得交点A.
解答 解:f(x)=$\frac{x}{{{e^{2x}}}}$的导数为f′(x)=$\frac{{e}^{2x}-2x{e}^{2x}}{({e}^{2x})^{2}}$=$\frac{1-2x}{{e}^{2x}}$,
可得曲线f(x)=$\frac{x}{{{e^{2x}}}}$在x=2处的切线斜率为f′(2)=$\frac{-3}{{e}^{4}}$,
切点为(2,$\frac{2}{{e}^{4}}$),
则曲线f(x)=$\frac{x}{{{e^{2x}}}}$在x=2处的切线方程为y-$\frac{2}{{e}^{4}}$=$\frac{-3}{{e}^{4}}$(x-2),
可令y=0,则x=$\frac{8}{3}$.
即有切线与x轴交点A的坐标为($\frac{8}{3}$,0).
点评 本题考查导数的运用:求切线方程,注意运用导数的运算法则和直线的点斜式方程,考查运算能力,属于基础题.

练习册系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{(\frac{1}{3})^{x}-2,x≤0}\end{array}\right.$,则不等式f(x)≥1的解集为( )
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|x≤-1或x≥3} | D. | {x|x≤0或x≥3} |
14.如图,正三棱柱(底面为正三角形,侧棱垂直底面)的正视图面积a2,则侧视图的面积为( )
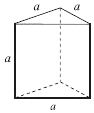

| A. | a2 | B. | $\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\sqrt{3}{a^2}$ | D. | $\frac{{\sqrt{3}}}{4}{a^2}$ |
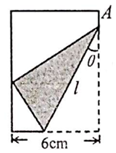 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,若$sinθ=\frac{1}{4}$,则折痕l的长度=$\frac{64}{5}$cm.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,若$sinθ=\frac{1}{4}$,则折痕l的长度=$\frac{64}{5}$cm.