题目内容
10.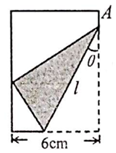 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,若$sinθ=\frac{1}{4}$,则折痕l的长度=$\frac{64}{5}$cm.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,若$sinθ=\frac{1}{4}$,则折痕l的长度=$\frac{64}{5}$cm.
分析 根据图形判断直角三角形,利用直角三角形求解AE=GEcos2θ=lsinθcos2θ,由AE+BE=lsinθcos2θ+lsinθ=6,求解即可.
解答 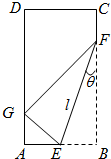 解:由已知及对称性知,GF=BF=lcosθ,GE=BE=lsinθ,
解:由已知及对称性知,GF=BF=lcosθ,GE=BE=lsinθ,
又∠GEA=∠GFB=2θ,
∴AE=GEcos2θ=lsinθcos2θ,
又由AE+BE=lsinθcos2θ+lsinθ=6得:l=$\frac{6}{sinθ(1+cos2θ)}$
=$\frac{6}{sinθ(2-2si{n}^{2}θ)}=\frac{6}{\frac{1}{4}×[2-2×(\frac{1}{4})^{2}]}$=$\frac{64}{5}$.
故答案为:$\frac{64}{5}$.
点评 本题考查了矩形的对折问题、直角三角形的边角关系、倍角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.椭圆$\frac{{x}^{2}}{3}$+y2=1上的点到直线x+y-4=0的最大距离是( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{4\sqrt{2}-\sqrt{6}}{2}$ | D. | 2$\sqrt{2}$-1 |
19.小明同学计划两次购买同一种笔芯(两次笔芯的单价不同),有两种方案:第一种方法是每次购买笔芯数量一定:第二种方法是每次购买笔芯所花钱数一定.则哪种购买方式比较经济( )
| A. | 第一种 | B. | 第二种 | C. | 两种一样 | D. | 无法判断 |
20.设集合U={0,1,2,3,4,5},A={0,1,3},B={1,2,5},则(∁UA)∩B=( )
| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |