题目内容
14．袋子中装有大小相同的4个球，其中2个红球和2个白球．游戏一，从袋中取一个球，若取出的是红球则甲获胜，否则乙获胜；游戏二，从袋中无放回地取一个球后再取一个球，若取出的两个球同色则甲获胜，否则乙获胜，则两个游戏（ ）| A． | 只有游戏一公平 | B． | 只有游戏二公平 | ||
| C． | 两个游戏都不公平 | D． | 两个游戏都公平 |
分析 由对立事件的概率计算公式求出每一种情况下甲乙胜的概率，比较概率大小得到结论．
解答 解：袋子中装有大小相同的4个球，其中2个红球和2个白球，游戏一，从袋中取一个球，若取出的是红球的概率为$\frac{1}{2}$，白球也是$\frac{1}{2}$，
故取出的是红球则甲获胜，否则乙获胜是公平的，
游戏二，从袋中无放回地取一个球后再取一个球，若取出的两个球同色，则甲获胜的概率为$\frac{2{C}_{2}^{1}{C}_{1}^{1}}{{C}_{4}^{1}{C}_{3}^{1}}$=$\frac{1}{3}$，则不公平，
故选：A．
点评 本题考查了古典概型及其概率计算公式，解答的关键是正确理解题意，求出基本事件总数和每一种事件发生的个数，是基础题．
练习册系列答案
相关题目
5．已知向量$\overrightarrow a=（{1，3}）$，$\overrightarrow b=（{-2，m}）$，若$\overrightarrow a$与$\overrightarrow a+2\overrightarrow b$平行，则m的值为（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | -6 |
2．设函数f（x）在R上存在导函数f′（x），对任意的实数x都有f（x）=2x2-f（-x），当x∈（-∞，0）时，f′（x）+1＜2x．若f（m+2）≤f（-m）+4m+4，则实数m的取值范围是（ ）
| A． | [-$\frac{1}{2}$，+∞） | B． | [-$\frac{3}{2}$，+∞） | C． | [-1，+∞） | D． | [-2，+∞） |
9．已知向量$\overrightarrow a=（1，1，0）$，$\overrightarrow b=（-1，0，2）$，且$k\overrightarrow a+\overrightarrow b$与$\overrightarrow a$互相垂直，则k=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $-\frac{1}{3}$ | D． | $-\frac{1}{2}$ |
19．
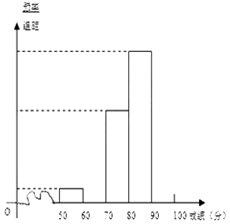中日“钓鱼岛争端”问题越来越引起社会关注，我校对高二600名学生进行了一次“钓鱼岛”知识测试，并从中抽取了部分学生的成绩（满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．
（1）填写频率分布表中的空格，补全频率分布直方图，并标出每个小矩形对应的纵轴数据；
（2）请你估算该年级学生成绩的中位数；
（3）如果用分层抽样的方法从样本分数在[60，70）和[80，90）的人中共抽取6人，再从6人中选2人，求2人分数都在[80，90）的概率．
中日“钓鱼岛争端”问题越来越引起社会关注，我校对高二600名学生进行了一次“钓鱼岛”知识测试，并从中抽取了部分学生的成绩（满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．| 分 组 | 频 数 | 频 率 |
| [50，60） | 2 | 0.04 |
| [60，70） | 8 | 0.16 |
| [70，80） | 10 | 0.2 |
| [80，90） | 16 | 0.32 |
| [90，100] | 14 | 0.28 |
| 合 计 | 50 | 1.00 |
（2）请你估算该年级学生成绩的中位数；
（3）如果用分层抽样的方法从样本分数在[60，70）和[80，90）的人中共抽取6人，再从6人中选2人，求2人分数都在[80，90）的概率．
6．点（x，y）满足$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤4\\ x，y∈N\end{array}\right.$，则点A落在区域C：x2+y2-4x-4y+7≤0内的概率为（ ）
| A． | $\frac{π}{16}$ | B． | $\frac{5}{16}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
3．已知由不等式$\left\{{\begin{array}{l}{x≥y}\\{y≥0}\\{x+y-4≤0}\end{array}}\right.$所确定的平面区域为M，由不等式x2+y2≤8所确定的平面区域为N，区域M内随机抽取一个点，该点同时落在区域N内的概率是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{16}$ | D． | $\frac{π}{4}$ |