题目内容
命题p:“对?x∈R,x2-2x+m≥0恒成立”,命题q:“方程
+
=1表示双曲线”.
(1)若p为假命题,求实数m的取值范围;
(2)若p∧q是假命题,p∨q是真命题,求实数m的取值范围.
| x2 |
| m-4 |
| y2 |
| 6-m |
(1)若p为假命题,求实数m的取值范围;
(2)若p∧q是假命题,p∨q是真命题,求实数m的取值范围.
考点:复合命题的真假,函数恒成立问题,双曲线的标准方程
专题:简易逻辑
分析:(1)先根据二次函数的图象求出命题p,为真命题时参数m的范围,根据p为假命题,求实数m的取值范围;
(2)先根据二次函数的图象及双曲线的方程满足条件求出命题p,q为真命题时参数m的范围,根据复合命题的真假与构成其简单命题真假的关系,由已知“p∧q是假命题,p∨q是真命题”得出p真q假或p假q真,求出m的范围.
(2)先根据二次函数的图象及双曲线的方程满足条件求出命题p,q为真命题时参数m的范围,根据复合命题的真假与构成其简单命题真假的关系,由已知“p∧q是假命题,p∨q是真命题”得出p真q假或p假q真,求出m的范围.
解答:
解:(1)若命题p真:
4-4m≤0解得m≥1,
∵p为假命题,
∴m<1,
∴实数m的取值范围为m<1,
(2)若命题p真:
4-4m≤0解得m≥1,
若命题q真:(m-4)(6-m)<0
∴m>6或m<4
∵p∧q是假命题,p∨q是真命题
∴p真q假或p假q真,
∴
或
解得m<1或4≤m≤6
∴实数m的取值范围m<1或4≤m≤6
4-4m≤0解得m≥1,
∵p为假命题,
∴m<1,
∴实数m的取值范围为m<1,
(2)若命题p真:
4-4m≤0解得m≥1,
若命题q真:(m-4)(6-m)<0
∴m>6或m<4
∵p∧q是假命题,p∨q是真命题
∴p真q假或p假q真,
∴
|
|
解得m<1或4≤m≤6
∴实数m的取值范围m<1或4≤m≤6
点评:本题考查复合命题的真假与构成其简单命题真假的关系,解决这类问题的关键是先求出两个简单命题为真命题时参数的范围,属于中档题.

练习册系列答案
相关题目
由a1=1,an+1=
给出的数列{an}的第33项是( )
| an |
| 3an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
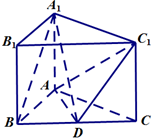 如图三棱柱ABC-A1B1C1中,侧棱与底面垂直,△ABC是等边三角形,点D是BC的中点.
如图三棱柱ABC-A1B1C1中,侧棱与底面垂直,△ABC是等边三角形,点D是BC的中点.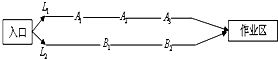 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是