题目内容
直线l1:ax-y+b=0,l2:bx-y+a=0(a、b≠0,a≠b)在同一坐标系中的图形大致是( )
A、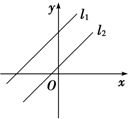 |
B、 |
C、 |
D、 |
考点:直线的一般式方程
专题:直线与圆
分析:首先将直线的一般式方程化为斜截式,根据斜率和截距之间的关系即可判断.
解答:
解:直线l1:ax-y+b=0可化为y=ax+b.
直线l2:bx-y+a=0可化为y=bx+a.
∵a≠b,
∴直线l1,l2不平行.故A不正确.
选项B中,截距b>0,a>0.
而斜率kl1=a<0.故B不正确.
选项D中,两直线斜率a>0,b>0.
而直线l1的截距b<0.故D不正确.
故选:C.
直线l2:bx-y+a=0可化为y=bx+a.
∵a≠b,
∴直线l1,l2不平行.故A不正确.
选项B中,截距b>0,a>0.
而斜率kl1=a<0.故B不正确.
选项D中,两直线斜率a>0,b>0.
而直线l1的截距b<0.故D不正确.
故选:C.
点评:本题考查直线的一般式方程和斜截式方程以及直线斜率、截距等知识,属于基础题.

练习册系列答案
相关题目
已知圆A:(x+2)2+y2=36,圆A内一定点B(2,0),圆P过B点且与圆A内切,则圆心P的轨迹为( )
| A、圆 | B、椭圆 |
| C、直线 | D、以上都不对 |
命题“若m>0,则关于x的方程x2+x-m=0有实数根”的逆否命题为( )
| A、若关于x的方程x2+x-m=0未找到引用源.有实数根,则m≤0 |
| B、若m≤0,则关于x的方程x2+x-m=0没有实数根 |
| C、若关于x的方程x2+x-m=0没有实数根,则m≤0 |
| D、若m>0,则关于x的方程x2+x-m=0没有实数根 |
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为( )
| α |
A、
| ||
B、
| ||
C、
| ||
D、
|
若数列{n(n+4)(
)n}中的最大项是第k项,则k=( )
| 2 |
| 3 |
| A、4 | B、5 | C、6 | D、7 |
大小为-
的角的终边落在( )
| 11π |
| 4 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,若a=2,c=4,B=60°,则b等于( )
A、2
| ||
| B、12 | ||
C、2
| ||
| D、28 |