题目内容
17.若tanα=2,tanβ=3,且α,β∈(0,$\frac{π}{2}$),则α+β的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{4}$ |
分析 由条件求得α+β的范围,再结合tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$ 的值,可得α+β的值.
解答 解:∵tanα=2,tanβ=3,且α,β∈(0,$\frac{π}{2}$),则α+β∈(0,π),
再根据tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=$\frac{5}{1-6}$=-1,∴α+β=$\frac{3π}{4}$.
故选:C.
点评 本题主要考查两角和的正切公式,根据三角函数的值求角,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
7.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
| A. | 若m⊥α,m⊥β,则α⊥β | B. | 若α⊥γ,β⊥γ,则α∥β | C. | 若m∥α,m∥β,则α∥β | D. | 若m⊥α,n∥α,则m⊥n |
8.直线y-1=k(x-1)(k∈R)与x2+y2-2y=0的位置关系( )
| A. | 相离或相切 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
5.设点P(x,y)是曲线a|x|+b|y|=1(a>0,b>0)上任意一点,其坐标(x,y)也满足$\sqrt{{x}^{2}+{y}^{2}+2x+1}$+$\sqrt{{x}^{2}+{y}^{2}-2x+1}$≤2$\sqrt{2}$,则$\sqrt{2}$a+b取值范围为( )
| A. | (0,2] | B. | [1,2] | C. | [1,+∞) | D. | [2,+∞) |
6.已知圆C1:x2+y2=4与圆C2:(x-1)2+(y-3)2=4,过动点P(a,b)分别作圆C1、圆C2的切线PM,PN,(M,N分别为切点),若|PM|=|PN|,则a2+b2-6a-4b+13的最小值是( )
| A. | 5 | B. | $\frac{8}{5}$ | C. | $\frac{2}{5}\sqrt{10}$ | D. | $\frac{1}{3}$ |
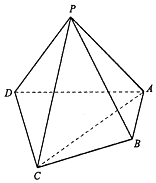 如图,在四凌锥中P-ABCD,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四凌锥中P-ABCD,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.