题目内容
6.已知圆C1:x2+y2=4与圆C2:(x-1)2+(y-3)2=4,过动点P(a,b)分别作圆C1、圆C2的切线PM,PN,(M,N分别为切点),若|PM|=|PN|,则a2+b2-6a-4b+13的最小值是( )| A. | 5 | B. | $\frac{8}{5}$ | C. | $\frac{2}{5}\sqrt{10}$ | D. | $\frac{1}{3}$ |
分析 根据条件PM=PN,求出P的轨迹方程,a2+b2-6a-4b+13=(a-3)2+(b-2)2的几何意义为P到定点(3,2)的距离的平方,即可得到结论.
解答 解:∵过动点P(a,b)分别作圆C1,圆C2的切线PM,PN( M、N分别为切点),若PM=PN,
∴|PC1|2=|PC2|2,
即a2+b2=(a-1)2+(b-3)2,
即a+3b-5=0,即动点P(a,b)在直线x+3y-5=0上,
a2+b2-6a-4b+13=(a-3)2+(b-2)2的几何意义为P到定点(3,2)的距离的平方,
则点(3,2)到直线x+3y-5=0的距离为$\frac{|3+6-5|}{\sqrt{1+9}}$=$\frac{4}{\sqrt{10}}$,
故a2+b2-6a-4b+13的最小值为$\frac{8}{5}$,
故选B.
点评 本题主要考查直线和圆的位置关系的应用,以及点到直线的距离公式的应用,利用距离的几何意义是解决本题的关键.

练习册系列答案
相关题目
17.若tanα=2,tanβ=3,且α,β∈(0,$\frac{π}{2}$),则α+β的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{4}$ |
1.如图矩形ABCD的长为2cm,宽为1cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( ) 

| A. | 10cm | B. | 8cm | C. | $(2\sqrt{3}+4)cm$ | D. | $4\sqrt{2}cm$ |
18.抛物线x2=4y的准线方程是( )
| A. | y=$\frac{1}{16}$ | B. | y=-$\frac{1}{16}$ | C. | y=x | D. | y=-1 |
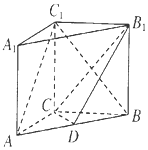 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.