题目内容
2.已知$f(x)=2+log_2^x,x∈[{\frac{1}{4},4}]$,试求y=[f(x)]2+f(x2)的值域[1,13].分析 根据$x∈[\frac{1}{4},4]$,求出y=[f(x)]2+f(x2)的定义域,利用换元法求解值域.
解答 解:由题意,$x∈[\frac{1}{4},4]$,
则f(x2)的定义域为[$\frac{1}{2}$,2],
故得函数y=[f(x)]2+f(x2)的定义域为[$\frac{1}{2}$,2].
∴y=(2+log2x)2+2+2log2x.
令log2x=t,(-1≤t≤1).
则y=(2+t)2+2t+2=t2+6t+6.
开口向上,对称轴t=-3.
∴当t=-1时,y取得最小值为1.
当t=1时,y取得最大值为13,
故得函数y的值域为[1,13].
故答案为[1,13].
点评 本题考查了复合函数的定义域的求法和利用换元法转化为二次函数问题求解值域的问题,属于基础题.

练习册系列答案
相关题目
17.若tanα=2,tanβ=3,且α,β∈(0,$\frac{π}{2}$),则α+β的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{4}$ |
7.“α=30°”是“sinα=$\frac{1}{2}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知圆C的圆心在x轴上,且经过A(5,2),B(-1,4)两点,则圆C的方程是( )
| A. | (x+2)2+y2=17 | B. | (x-2)2+y2=13 | C. | (x-1)2+y2=20 | D. | (x+1)2+y2=40 |
 如图,椭圆E的左、右焦点分别为F1,F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P,Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为$\frac{1}{3}$或$\frac{5}{7}$.
如图,椭圆E的左、右焦点分别为F1,F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P,Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为$\frac{1}{3}$或$\frac{5}{7}$.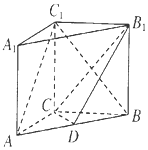 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.