题目内容
1.不等式组$\left\{\begin{array}{l}{2x+y-3≤0}\\{3x-y+3≥0}\\{x-2y+1≤0}\end{array}\right.$的解集记为D,有下面四个命题:p1:?(x,y)∈D,2x+3y≥-1;
p2:?(x,y)∈D,2x-5y≥-3;
p3:?(x,y)∈D,$\frac{y-1}{2-x}$≤$\frac{1}{3}$;
p4:?(x,y)∈D,x2+y2+2y≤1.
其中的真命题是( )
| A. | p1,p2 | B. | p2,p3 | C. | p2,p4 | D. | p3,p4 |
分析 画出约束条件不是的可行域,利用目标函数的几何意义,求出范围,判断选项的正误即可.
解答 解:不等式组$\left\{\begin{array}{l}{2x+y-3≤0}\\{3x-y+3≥0}\\{x-2y+1≤0}\end{array}\right.$的可行域如图: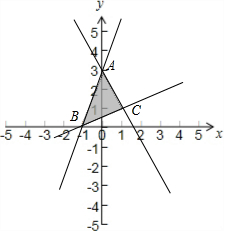
p1:B(-1,0)点,2x+3y=-2,
故?(x,y)∈D,2x+3y≥-1为假命题;
p2:B(-1,0)点,2x-5y=-2,
故?(x,y)∈D,2x-5y≥-3为真命题;
p3:A(0,3)点,$\frac{y-1}{2-x}$=1,
故?(x,y)∈D,$\frac{y-1}{2-x}$≤$\frac{1}{3}$为假命题;
p4:B(-1,0)点,x2+y2+2y=1
故?(x,y)∈D,x2+y2+2y≤1为真命题.
可得选项p2,p4正确.
故选:C
点评 本题考查线性规划的解得应用,命题的真假的判断,正确画出可行域以及目标函数的几何意义是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
10.在等差数列{an}中,a4=1,a7+a9=16,a12=( )
| A. | 31 | B. | 30 | C. | 16 | D. | 15 |
11.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
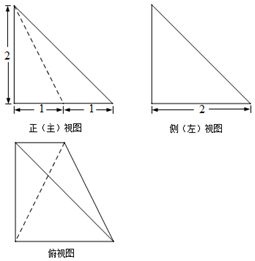

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |