题目内容
9.圆心在(1,1)的圆截直线y=x-2所得的弦长为2$\sqrt{2}$,则这个圆的方程为(x-1)2+(y-1)2=4.分析 由条件求出弦心距,再利用弦长公式求出半径,即可求得圆的标准方程.
解答 解:设半径为r,由于弦长l=2$\sqrt{2}$,弦心距d=$\frac{|1-1-2|}{\sqrt{2}}$=$\sqrt{2}$,
∴r=$\sqrt{{d}^{2}+(\frac{l}{2})^{2}}$=$\sqrt{2+2}$=2,
故圆的方程为 (x-1)2+(y-1)2=4.
故答案为:(x-1)2+(y-1)2=4.
点评 本题主要考查直线和圆的位置关系,求圆的标准方程,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),P为双曲线上任一点,若双曲线的离心率的取值范围为[$\sqrt{2}$,2],则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$最小值的取值范围是( )
| A. | [$\frac{1}{2}$,$\frac{3}{4}$] | B. | [-$\frac{3}{4}$,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,-$\frac{1}{4}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$] |
3.在△ABC中,∠BAC=120°,AB=2,AC=1,D是边BC上的点,且|BD|=2|DC|,则$\overrightarrow{AD}$•$\overrightarrow{BC}$的值为( )
| A. | 0 | B. | 1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
1.下列有关命题的说法正确的是( )
| A. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| B. | 命题“若x=y,则sin x=sin y”的逆否命题为真命题 | |
| C. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| D. | 命题“?x∈R,使得:x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
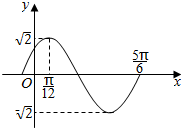 函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.