在△ABC中.∠BAC=120°.AB=2.AC=1.D是边BC上的点.且|BD|=2|DC|.则$\overrightarrow{AD}$•$\overrightarrow{BC}$的值为( )A．0B．1C．$\frac{1}{3}$D．-$\frac{1}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

3．在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上的点，且|BD|=2|DC|，则$\overrightarrow{AD}$•$\overrightarrow{BC}$的值为（　　）

A．

B．

C．

$\frac{1}{3}$

D．

-$\frac{1}{3}$

分析建立平面直角坐标系，求出向量坐标，代入公式计算．

解答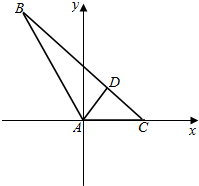解：建立如图所示的坐标系，则A（0，0），B（-1，$\sqrt{3}$），C（1，0），D（$\frac{1}{3}$，$\frac{\sqrt{3}}{3}$）．
∴$\overrightarrow{AD}$=（$\frac{1}{3}$，$\frac{\sqrt{3}}{3}$），$\overrightarrow{BC}$=（2，-$\sqrt{3}$）．∴$\overrightarrow{AD}$•$\overrightarrow{BC}$=$\frac{1}{3}×2$-$\frac{\sqrt{3}}{3}$×$\sqrt{3}$=-$\frac{1}{3}$．
故选：D．

点评本题考查了平面向量的数量积运算，建立坐标系可使计算简便．

练习册系列答案

12．已知{a_n}是公差为d的等差数列，它的前n项和为S_n，S₄=2S₂+4，${b_n}=\frac{{1+{a_n}}}{a_n}$．
（1）求公差d的值；
（2）若${a_1}=-\frac{5}{2}$，求数列{b_n}中的最大项和最小项的值；
（3）若对任意的n∈N^*，都有b_n≤b₈成立，求a₁的取值范围．
（4）若对任意的n∈N^*，数列{b_n}中最小值为b₈，求a₁的取值范围．

9．圆心在（1，1）的圆截直线y=x-2所得的弦长为2$\sqrt{2}$，则这个圆的方程为（x-1）²+（y-1）²=4．

16．将函数f（x）=$\sqrt{3}$sin3x+cos3x的图象向左平移$\frac{π}{6}$个单位得到函数g（x）的图象，关于函数g（x），下列说法正确的是（　　）

	A．	在[$\frac{π}{4}$，$\frac{π}{2}$]上是增函数
	B．	其图象关于直线x=-$\frac{π}{4}$对称
	C．	函数g（x）是奇函数
	D．	当x$∈[\frac{π}{3}，\frac{4π}{9}]$时，函数g（x）的值域是[-$\sqrt{3}$，0]

8．用与球心距离为2的平面去截球，所得的截面面积为π，则球的表面积为（　　）

15．