题目内容
15.已知函数$f(x)=\frac{1}{3}{x^3}-\frac{a}{2}{x^2}+x-3$有两个极值点,则a的范围(-∞,-2)∪(2,+∞).分析 求导f′(x)=x2-ax+1,由函数f(x)有两个极值点,则方程f′(x)=0,有两个不相等的根,则△>0,即可求得a的范围.
解答 解:由题意可知:函数$f(x)=\frac{1}{3}{x^3}-\frac{a}{2}{x^2}+x-3$,求导,f′(x)=x2-ax+1,
由函数f(x)有两个极值点,
则方程f′(x)=0,有两个不相等的根,
∴△>0,即a2-4>0,解得:a>2或a<-2,
∴a的范围(-∞,-2)∪(2,+∞),
故答案为:(-∞,-2)∪(2,+∞).
点评 本题考查导数的应用,函数极值存在的条件,考查一元二次函数的个数,考查转化思想,属于基础题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
20.设a,b是两条直线α,β是两个平面,则“a?α,b⊥β,α∥β”是“a⊥b”的( )
| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
20.已知定义在R上的函数f(x)满足f(x)=f(4-x),且当x≥2时,f(x)=4x+2x-6,则f(x)在区间[0,4]上的最大值与最小值分别为( )
| A. | 266,14 | B. | 256,14 | C. | 256,-$\frac{21}{4}$ | D. | 266,-4 |
 已知长方体ABCD-A1B1C1D1中,AD=AB=2,AA1=1,E为C1D1的中点.
已知长方体ABCD-A1B1C1D1中,AD=AB=2,AA1=1,E为C1D1的中点.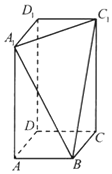 长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$
长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$