题目内容
10.已知函数f(x)=x3+ax2+x+2.(Ⅰ)若a=-1,令函数g(x)=2x-f(x),求函数g(x)的极大值和极小值;
(Ⅱ)若函数f(x)在(-$\frac{1}{3}$,+∞)上恒为单调递增函数,求实数a的取值范围.
分析 (Ⅰ)先求出函数g(x)=x-x3+x2-2,的导函数,利用导函数求出原函数的单调区间,进而求出其极大值、极小值;
(Ⅱ)先求出其导函数,把函数f(x)在(-$\frac{1}{3}$,+∞)上恒为单调递增函数,转化为其导函数的最小值恒大于等于0,利用二次函数在固定区间上求最值的方法求出导函数的最小值,再与0比即可求出实数a的取值范围.
解答 解:(Ⅰ)当a=-1,f(x)=x3-x2+x+2,g(x)=x-x3+x2-2,求导,g′(x)=-3x2+2x+1,
令g′(x)=0,解得:x=-$\frac{1}{3}$,x=1,
| x | (-∞,-$\frac{1}{3}$) | -$\frac{1}{3}$ | (-$\frac{1}{3}$,1) | 1 | (1,+∞) |
| g′(x) | - | 0 | + | 0 | - |
| g(x) | ↘ | -$\frac{59}{27}$ | ↗ | -1 | ↘ |
(Ⅱ)f′(x)=3x2+2ax+1的对称轴为x=-$\frac{a}{3}$
①若-$\frac{a}{3}$≥-$\frac{1}{3}$,即a≤1时,要使f(x)在(-$\frac{1}{3}$,+∞)上单调递增,则有
△=4a2-12≤0,则-$\sqrt{3}$$≤a≤\sqrt{3}$
∴-$\sqrt{3}$≤a≤1
②若-$\frac{a}{3}<-\frac{1}{3}$,即a>1时,由题知f(-$\frac{1}{3}$)≥0,则a≤2
∴1<a≤2,
综上可知:a的取值范围,(-$\sqrt{3}$,2).
点评 本题考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值,属于中档题.

练习册系列答案
相关题目
14.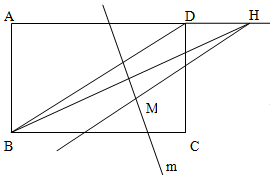 如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )
如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )
 如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )
如图所示,ABCD是长为8,宽为4的矩形,设点H在直线AD上运动,BH的垂直平分线为m,过点H且与BD平行(或重合)的直线与直线m相交于点M,则点M的轨迹为( )| A. | 圆的一部分 | B. | 椭圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
15.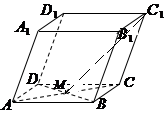 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )| A. | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
2.3<m<5是方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m-3}$=1表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.如果抛物线方程为y2=4x,那么它的焦点坐标为( )
| A. | (1,0) | B. | (2,0) | C. | (-1,0) | D. | (-2,0) |