题目内容
3．已知a、b、c∈R，试讨论函数f（x）=ax2+bx+c的单调性．分析 讨论a=0，再b是否为0，结合一次函数的单调性；讨论a＞0，a＜0时，由二次函数的单调性，即可得到．
解答 解：（1）若a=0，
①b=0，则f（x）=c为常数函数，无单调性；
②若b＞0，则f（x）在R上为增函数；
③若b＜0，则f（x）在R上为减函数；
（2）若a≠0，
①a＞0，则f（x）的对称轴为x=-$\frac{b}{2a}$，f（x）在（-∞，-$\frac{b}{2a}$）为减函数，
在（-$\frac{b}{2a}$，+∞）为增函数；
②a＜0，则f（x）的对称轴为x=-$\frac{b}{2a}$，f（x）在（-∞，-$\frac{b}{2a}$）为增函数，
在（-$\frac{b}{2a}$，+∞）为减函数．
点评 本题考查函数的单调性的判断，注意运用分类讨论的思想方法，考查推理能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．函数f（x）=|cosx|的最小正周期为（ ）
| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
8．已知x1＞0，x2＞0，x1+x2＜ex1x2（e为自然对数的底数），则（ ）
| A． | x1+x2＞1 | B． | x1+x2＜1 | C． | $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$＜$\frac{1}{e}$ | D． | $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$＞$\frac{1}{e}$ |
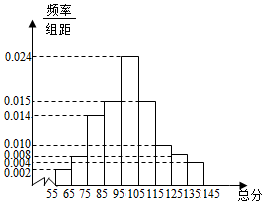从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分布直方图．
8．复数$\frac{{i（{-6+i}）}}{{|{3-4i}|}}$的实部与虚部之差为（ ）
| A． | -1 | B． | 1 | C． | $-\frac{7}{5}$ | D． | $\frac{7}{5}$ |