Question

5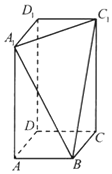．长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，过A₁，C₁，B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A₁C₁D₁，这个几何体的体积为$\frac{40}{3}$
（1）求证：直线A₁B∥平面CDD₁C₁
（2）求证：平面ACD₁∥平面A₁BC₁
（3）求棱A₁A的长．

Answer 1

分析 （1）如图，连接D₁C，已知ABCD-A₁B₁C₁D₁是长方体，可证四边形A₁BCD₁是平行四边形，再利用直线与平面平行的判定定理进行证明，即可解决问题；
（2）连接AD₁，AC，由（1）得A₁B∥D₁C，又∵A₁C₁∥AC
（3）设A₁A=h，已知几何体ABCD-A₁C₁D₁的体积为$\frac{40}{3}$，利用等体积法VABCD-A₁C₁D₁=VABCD-A₁B₁C₁D₁-VB-A₁B₁C₁，进行求解．

解答 解：（1）证明：如图，连接D₁C，
∵ABCD-A₁B₁C₁D₁是长方体，
∴A₁D₁∥BC且A₁D₁=BC．
∴四边形A₁BCD₁是平行四边形．
∴A₁B∥D₁C．
∵A₁B?平面CDD₁C₁，D₁C?平面CDD₁C₁，
∴A₁B∥平面CDD₁C₁．
（2）证明：连接AD₁，AC
由（1）得A₁B∥D₁C，又∵A₁C₁∥AC
A₁C₁∩A₁B=A₁，A₁C₁、A₁B?面A₁BC₁
AC∩D₁C=C，AC、D₁C?面ACD₁．
平面ACD₁∥平面A₁BC₁
（3）设A₁A=h，∵几何体ABCD-A₁C₁D₁的体积为$\frac{40}{3}$，即S_ABCD×h-$\frac{1}{3}$×S△A₁B₁C₁×h=$\frac{40}{3}$，
即2×2×h-$\frac{1}{3}×\frac{1}{2}$×2×2×h=$\frac{40}{3}$，解得h=4．
∴A₁A的长为4．

点评 本题主要考查空间线面的位置关系、运算求解能力和探究能力，同时考查学生灵活利用图形，属于中档题．