题目内容
20.设a,b是两条直线α,β是两个平面,则“a?α,b⊥β,α∥β”是“a⊥b”的( )| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
分析 根据空间直线和平面的位置关系结合充分条件和必要条件的定义进行判断即可.
解答 解:若α∥β,则当b⊥β时,b⊥α,
∵a?α,∴a⊥b成立,即充分性成立,
若a⊥b,则a?α,b⊥β,α∥β不一定成立,即必要性不成立,
则“a?α,b⊥β,α∥β”是“a⊥b”的充分不必要条件,
故选:C
点评 本题主要考查充分条件和必要条件的判断,根据空间直线和平面的位置关系是解决本题的关键.

练习册系列答案
相关题目
10.已知O为坐标原点,F是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点,A、B分别为椭圆C的左、右顶点,P为椭圆C上一点,且PF⊥x轴.过顶点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.已知x1>0,x2>0,x1+x2<ex1x2(e为自然对数的底数),则( )
| A. | x1+x2>1 | B. | x1+x2<1 | C. | $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$<$\frac{1}{e}$ | D. | $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$>$\frac{1}{e}$ |
15.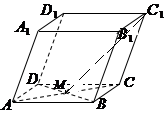 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
 四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )
四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{C_1}M}$可以表示为( )| A. | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
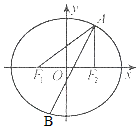 椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$.
椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$.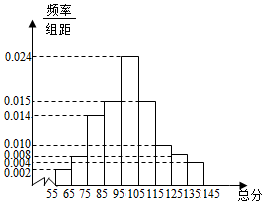 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.