题目内容
8.直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2$\sqrt{2}$,则三棱柱ABC-A1B1C1的外接球的表面积为( )| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
分析 由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,我们可以把直三棱柱ABC-A1B1C1补成四棱柱,则四棱柱的体对角线是其外接球的直径,求出外接球的直径后,代入外接球的表面积公式,即可求出该三棱柱的外接球的表面积.
解答  解:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
解:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
把直三棱柱ABC-A1B1C1补成四棱柱,
则四棱柱的体对角线是其外接球的直径,
所以外接球半径为$\frac{1}{2}\sqrt{8+4}$=$\sqrt{3}$,
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=12π.
故选:D.
点评 在求一个几何体的外接球表面积(或体积)时,关键是求出外接球的半径,我们通常有如下办法:①构造三角形,解三角形求出R;②找出几何体上到各顶点距离相等的点,即球心,进而求出R;③将几何体补成一个长方体,其对角线即为球的直径,进而求出R.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
19.已知边长为a的菱形ABCD中,∠ABC=60°,将该菱形沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为( )
| A. | $\frac{a^3}{6}$ | B. | $\frac{a^3}{12}$ | C. | $\frac{{\sqrt{3}{a^3}}}{12}$ | D. | $\frac{{\sqrt{2}{a^3}}}{12}$ |
16.已知两个不同直线a,b,两不同平面α,β,下列结论正确的是( )
| A. | 若a∥b,a∥α,则b∥α | B. | 若a⊥b,a⊥α,则b⊥α | ||
| C. | 若a∥α,a∥β,α∩β=b,则a∥b | D. | 若a∥α,α⊥β,则a⊥β |
4.已知x,y满足不等式组$\left\{\begin{array}{l}y≤x+1\\ y≥0\\ x≤1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
2.已知函数f(x)=$\left\{\begin{array}{l}sin({x+α}),({x≤0})\\ cos({x-β}),({x>0})\end{array}$是偶函数,则下列结论可能成立的是( )
| A. | $α=\frac{π}{4},β=\frac{π}{8}$ | B. | $α=\frac{2π}{3},β=\frac{π}{6}$ | C. | $α=\frac{π}{3},β=\frac{π}{6}$ | D. | $α=\frac{5π}{6},β=\frac{2π}{3}$ |
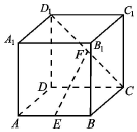 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.