题目内容
20.已知数列{an}是首项为1的单调递增的等比数列,且满足a3,$\frac{5}{3}$a4,a5成等差数列.(Ⅰ)求{an}的通项公式;
(Ⅱ)设数列{$\frac{2n-1}{{a}_{n}}$}的前n项和Sn,求证:Sn<3.
分析 (1)由已知列关于公比q的方程组,求解得到q值,则等比数列的通项公式可求;
(2)把{an}的通项公式代入数列{$\frac{2n-1}{{a}_{n}}$},利用错位相减法求其和,可得Sn<3.
解答 (1)解:由${a}_{3}+{a}_{5}=2×\frac{5}{3}{a}_{4}$,得${q}^{2}+{q}^{4}=\frac{10}{3}{q}^{3}$,
而q≠0,得3q2-10q+3=0,解得q=$\frac{1}{3}$或q=3.
∵数列{an}是首项为1的单调递增的等比数列,
∴q=3,则${a_n}={3^{n-1}}$;
(2)证明:由$\frac{2n-1}{{a}_{n}}=\frac{2n-1}{{3}^{n-1}}$,
∴${S_n}=1+\frac{3}{3}+\frac{5}{3^2}+\frac{7}{3^3}+…+\frac{2n-1}{{{3^{n-1}}}}$,①
∴$\frac{1}{3}{S_n}=\frac{1}{3}+\frac{3}{3^2}+\frac{5}{3^3}+\frac{7}{3^4}+…+\frac{2n-1}{3^n}$,②
①-②得:$\frac{2}{3}{S_n}=1+2({\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+…+\frac{1}{{{3^{n-1}}}}})-\frac{2n-1}{3^n}$=$1+2×\frac{\frac{1}{3}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}=\frac{2n-1}{{3}^{n-1}}$,
得${S_n}=3-\frac{n+1}{{{3^{n-1}}}}$<3.
∴Sn<3.
点评 本题考查数列递推式,考查了等比数列通项公式的求法,训练了错位相减法求数列的和,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 36πcm3 | B. | 12πcm3 | C. | 9πcm3 | D. | 72πcm3 |
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.5 |
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
| A. | 14 | B. | 15 | C. | 14或15 | D. | 15或16 |
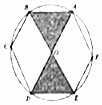 已知正六边形ABCDEF内接于圆O,连接AD,BE,现在往圆O内投掷2000粒小米,则可以估计落在阴影区域内的小米的粒数大致是( )(参考数据:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)
已知正六边形ABCDEF内接于圆O,连接AD,BE,现在往圆O内投掷2000粒小米,则可以估计落在阴影区域内的小米的粒数大致是( )(参考数据:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)