题目内容
11.在多项式(3$\sqrt{x}$-$\frac{2}{\root{3}{x}}$)4($\sqrt{x}$+2x)5的展开式中,含x2项的系数为( )| A. | -32 | B. | 32 | C. | -96 | D. | 96 |
分析 化(3$\sqrt{x}$-$\frac{2}{\root{3}{x}}$)4($\sqrt{x}$+2x)5=${(3\sqrt{x}-\frac{2}{\root{3}{x}})}^{4}$•${x}^{\frac{5}{2}}$•${(1+2\sqrt{x})}^{5}$;
在${(3\sqrt{x}-\frac{2}{\root{3}{x}})}^{4}$展开式中,利用通项公式求出展开式各项,得出符合条件的项,
即可求出多项式展开式中含x2项的系数.
解答 解:(3$\sqrt{x}$-$\frac{2}{\root{3}{x}}$)4($\sqrt{x}$+2x)5=${(3\sqrt{x}-\frac{2}{\root{3}{x}})}^{4}$•${x}^{\frac{5}{2}}$•${(1+2\sqrt{x})}^{5}$;
在${(3\sqrt{x}-\frac{2}{\root{3}{x}})}^{4}$展开式中,通项公式为
Tr+1=${C}_{4}^{r}$•${(3\sqrt{x})}^{4-r}$•${(-\frac{2}{\root{3}{x}})}^{r}$=34-r•(-2)r•${C}_{4}^{r}$•${x}^{2-\frac{5r}{6}}$;
令r=0,其展开式中是x2,不合题意;
令r=1,其展开式中是${x}^{\frac{1}{6}}$,不合题意;
令r=2,其展开式中是${x}^{\frac{1}{3}}$,不合题意;
令r=3,其展开式中是${x}^{-\frac{1}{2}}$,符合题意,
且含x2项的系数为3•(-2)3•${C}_{4}^{3}$=-96;
令r=4,其展开式中是${x}^{-\frac{4}{3}}$,不合题意;
综上,多项式(3$\sqrt{x}$-$\frac{2}{\root{3}{x}}$)4($\sqrt{x}$+2x)5的展开式中,含x2项的系数为-96.
故选:C.
点评 本题考查了二项式展开式通项公式的应用问题,是基础题.

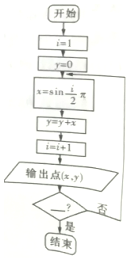
| A. | i>8 | B. | i>7 | C. | i>6 | D. | i>5 |
| A. | [-$\frac{1}{12}$,0] | B. | [-$\frac{1}{12}$,-$\frac{4}{49}$) | C. | (-$\frac{4}{49}$,0] | D. | [-$\frac{4}{49}$,0] |
| A. | c<a<b | B. | a<b<c | C. | b<c<a | D. | b<a<c |
| A. | 2 | B. | -2 | C. | ±2 | D. | ±3 |