题目内容
10.已知函数f(x)=2ax3-(3a+1)x2+2x+5;(1)a为何值时,函数f(x)没有极值点;
(2)讨论函数f(x)的单调性.
分析 (1)求出函数的导数,根据题意只需f′(x)≥0即可求出a的值;
(2)通过讨论a的范围,求出函数的单调区间即可.
解答 解:(1)f′(x)=6ax2-2(3a+1)x+1=2(3ax-1)(x-1),
∴3a=1,a=$\frac{1}{3}$时无极值点;
(2)由(1)得:
①a>$\frac{1}{3}$时,$\frac{1}{3a}$<1,
f(x)在(-∞,$\frac{1}{3a}$),(1,+∞)递增,在($\frac{1}{3a}$,1)递减,
②a=$\frac{1}{3}$时,f(x)在R递增,
③0<a<$\frac{1}{3}$时,1<$\frac{1}{3a}$,
f(x)在(-∞,1,),($\frac{1}{3a}$+∞)递增,在(1,$\frac{1}{3a}$)递减,
④当a=0时,f(x)=-(x-1),
f(x)在(-∞,1)递增,在(1,+∞)递减,
⑤a<0时,$\frac{1}{3a}$<1,
f(x)在(-∞,$\frac{1}{3a}$),(1,+∞)递减,在($\frac{1}{3a}$,1)递增.
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
1.运行如图所示的程序框图,若输出的点恰有3次落在直线上y=x,则判断框中可填写的条件是( )
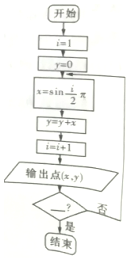

| A. | i>8 | B. | i>7 | C. | i>6 | D. | i>5 |
18.已知集合M={x∈Z|x<3},N={x|1≤ex≤e},则M∩N等于( )
| A. | ∅ | B. | {0} | C. | [0,1] | D. | {0,1} |
2.已知集合A={x|ax2+x-3=0},B={x|3≤x<7},若A∩B≠∅,则实数a的取值集合为( )
| A. | [-$\frac{1}{12}$,0] | B. | [-$\frac{1}{12}$,-$\frac{4}{49}$) | C. | (-$\frac{4}{49}$,0] | D. | [-$\frac{4}{49}$,0] |