题目内容
9.已知函数f(x)=-x2-6x-3,设max{p,q}表示p,q二者中较大的一个.函数g(x)=max{($\frac{1}{2}$)x-2,log2(x+3)}.若m<-2,且?x1∈[m,-2),?x2∈(0,+∞),使得f(x1)=g(x2)成立,则m的最小值为( )| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
分析 求出g(x),作函数y=f(x)的图象,如图所示,f(x)=2时,方程两根分别为-5和-1,即可得出结论.
解答 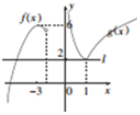 解:由题意,g(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-2},0<x<1}\\{lo{g}_{2}(x+3),x≥1}\end{array}\right.$,∴g(x)min=g(1)=2,f(x)=-(x-3)2+6≤6,
解:由题意,g(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-2},0<x<1}\\{lo{g}_{2}(x+3),x≥1}\end{array}\right.$,∴g(x)min=g(1)=2,f(x)=-(x-3)2+6≤6,
作函数y=f(x)的图象,如图所示,f(x)=2时,方程两根分别为-5和-1,则m的最小值为-5.
故选A.
点评 本题主要考查了函数的等价转化思想,数形结合的数学思想,以及函数求值域的方法,属中等题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0,2$\sqrt{2}$)是抛物线C上一点,圆M与y轴相切且与线段MF相交于点A,若$\frac{|MA|}{|AF|}$=2,则p=2.
14.某中学是走读中学,为了让学生更有效率利用下午放学后的时间,学校在本学期第一次月考后设立了多间自习室,以便让学生在自习室自主学习、完成作业,同时每天派老师轮流值班.在本学期第二次月考后,高一某班数学老师统计了两次考试该班数学成绩优良人数和非优良人数,得到如下2×2列联表:
(1)能否在在犯错误的概率不超过0.005的前提下认为设立自习室对提高学生成绩有效;
(2)从该班第一次月考的数学优良成绩中和第二次月考的数学非优良成绩中,按分层抽样随机抽取5个成绩,再从这5个成绩中随机抽取2个,求这2个成绩来自同一次月考的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 非优良 | 优良 | 总计 | |
| 未设立自习室 | 25 | 15 | 40 |
| 设立自习室 | 10 | 30 | 40 |
| 总计 | 35 | 45 | 80 |
(2)从该班第一次月考的数学优良成绩中和第二次月考的数学非优良成绩中,按分层抽样随机抽取5个成绩,再从这5个成绩中随机抽取2个,求这2个成绩来自同一次月考的概率.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.在等比数列{an}中,首项a1=1,若数列{an}的前n项之积为Tn,且T5=1024,则该数列的公比的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±3 |
18.命题“?x>0,lnx≤x-1”的否定是( )
| A. | ?x0>0,lnx0≤x0-1 | B. | ?x0>0,lnx0>x0-1 | C. | ?x0<0,lnx0<x0-1 | D. | ?x0>0,lnx0≥x0-1 |
19.已知直线ax+by-8=0(a>0,b>0)被圆x2+y2-2x-4y=0截得的弦长为2$\sqrt{5}$,则ab的最大值是( )
| A. | $\frac{5}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 8 |