题目内容
12．设函数f（x）=-x2+14x+15，数列{an}满足an=f（n），n∈N+，数列{an}的前n项和Sn最大时，n=（ ）| A． | 14 | B． | 15 | C． | 14或15 | D． | 15或16 |
分析 由题意，-n2+14n+15≥0，得-1≤n≤15，即可得出结论．
解答 解：由题意，-n2+14n+15≥0，∴-1≤n≤15，
∴数列{an}的前n项和Sn最大时，n=14或15．
故选：C．
点评 本题考查数列的函数性质，考查学生解不等式的能力，比较基础．
练习册系列答案
相关题目
2．已知集合A={x|ax2+x-3=0}，B={x|3≤x＜7}，若A∩B≠∅，则实数a的取值集合为（ ）
| A． | [-$\frac{1}{12}$，0] | B． | [-$\frac{1}{12}$，-$\frac{4}{49}$） | C． | （-$\frac{4}{49}$，0] | D． | [-$\frac{4}{49}$，0] |
7．设集合A={x∈R|x-1＞0}，B={x∈R|x＜0}，C={x∈R|x（x-1）＞0}，则“x∈A∪B“是“x∈C“的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
4．已知抛物线C：y2=2px（p＞0）的焦点为F，点M（x0，2$\sqrt{2}$）是抛物线C上一点，圆M与y轴相切且与线段MF相交于点A，若$\frac{|MA|}{|AF|}$=2，则p=2．
1．在等比数列{an}中，首项a1=1，若数列{an}的前n项之积为Tn，且T5=1024，则该数列的公比的值为（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | ±3 |
2．
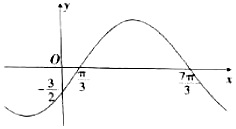已知函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，将函数y=f（x）的图象向左平移$\frac{4π}{3}$个单位，得到函数y=g（x）的图象，则函数y=g（x）在区间$[{\frac{π}{2}，\frac{5π}{2}}]$上的最大值为（ ）
已知函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，将函数y=f（x）的图象向左平移$\frac{4π}{3}$个单位，得到函数y=g（x）的图象，则函数y=g（x）在区间$[{\frac{π}{2}，\frac{5π}{2}}]$上的最大值为（ ）| A． | 3 | B． | $\frac{{3\sqrt{3}}}{2}$ | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |