题目内容
已知圆C1:(x+1)2+y2=16,点C2(1,0),点Q在圆C1上运动,QC2的垂直平分线交QC1于点H.
(Ⅰ)求动点H的轨迹C的方程;
(Ⅱ)若曲线C与x轴交于A、B两点,过点C1的直线交曲线C于M、N两点,记△ABM与△ABN的面积分别为S1和S2,求|S1-S2|的最大值.
(Ⅰ)求动点H的轨迹C的方程;
(Ⅱ)若曲线C与x轴交于A、B两点,过点C1的直线交曲线C于M、N两点,记△ABM与△ABN的面积分别为S1和S2,求|S1-S2|的最大值.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(I)由QC2的垂直平分线交QC1于H,可得|HQ|=|HC2|,从而|HC2|+|HC1|=|HC1|+|HQ|=|QC1|=4>|C1C2|=2,可得动点H的轨迹是点C1,C2为焦点的椭圆,由此能够求出椭圆的标准方程.
(Ⅱ)分类讨论,设出直线方程,代入椭圆方程,利用韦达定理,表示出|S1-S2|,利用基本不等式可求最大值.
(Ⅱ)分类讨论,设出直线方程,代入椭圆方程,利用韦达定理,表示出|S1-S2|,利用基本不等式可求最大值.
解答:
解:(Ⅰ)∵QC2的垂直平分线交QC1于H,
∴|HQ|=|HC2|,
∴|HC2|+|HC1|=|HC1|+|HQ|=|QC1|=4>|C1C2|=2,
∴动点H的轨迹是点C1,C2为焦点的椭圆,且2a=4,2c=2,∴b2=3,
∴椭圆的标准方程是
+
=1;
(Ⅱ)当直线斜率不存在时,直线方程为x=-1,此时△ABM与△ABN的面积相等,|S1-S2|=0;
当直线斜率存在时,设直线方程为y=k(x+1)(k≠0),M(x1,y1),N(x2,y2),
直线方程代入椭圆方程,消去y可得(3+4k2)x2+8k2x+4k2-12=0,
∴x1+x2=-
,x1x2=
,
∴|S1-S2|=2|y1+y2|=2|k(x1+x2)+2k|=
∵k≠0,∴|S1-S2|=
≤
=
,
当且仅当k=±
时等号成立,故|S1-S2|的最大值
.
∴|HQ|=|HC2|,
∴|HC2|+|HC1|=|HC1|+|HQ|=|QC1|=4>|C1C2|=2,
∴动点H的轨迹是点C1,C2为焦点的椭圆,且2a=4,2c=2,∴b2=3,
∴椭圆的标准方程是
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)当直线斜率不存在时,直线方程为x=-1,此时△ABM与△ABN的面积相等,|S1-S2|=0;
当直线斜率存在时,设直线方程为y=k(x+1)(k≠0),M(x1,y1),N(x2,y2),
直线方程代入椭圆方程,消去y可得(3+4k2)x2+8k2x+4k2-12=0,
∴x1+x2=-
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∴|S1-S2|=2|y1+y2|=2|k(x1+x2)+2k|=
| 12|k| |
| 3+4k2 |
∵k≠0,∴|S1-S2|=
| 12 | ||
|
| 12 | ||
2
|
| 3 |
当且仅当k=±
| ||
| 2 |
| 3 |
点评:本题考查圆的性质和应用,考查直线与椭圆的位置关系,考查基本不等式的运用,考查韦达定理,正确运用韦达定理是关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
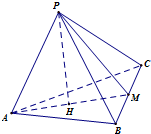 (理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).
(理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示). 已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.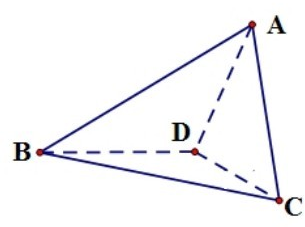 已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.
已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.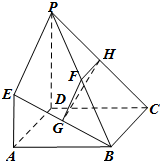 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.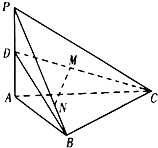 如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2
如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2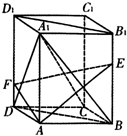 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.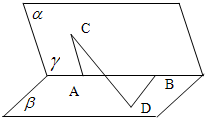 如图,在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为