题目内容
7.已知f(x)=x+$\frac{9}{x}$在区间[1,4]上的最小值为n,则二项式(x-$\frac{1}{x}$)n展开式中x2的系数为15.分析 利用导数研究函数f(x)的单调性,即可得出最小值.再利用二项式定理的通项公式即可得出.
解答 解:f′(x)=1-$\frac{9}{{x}^{2}}$=$\frac{(x+3)(x-3)}{{x}^{2}}$,x∈[1,4].
令f′(x)=0,解得x=3.∴x∈[1,3]时,函数f(x)单调递减;x∈(3,4]时,函数f(x)单调递增.
∴x=3时,函数f(x)取得最小值6.
∴$(x-\frac{1}{x})^{6}$的通项公式:Tr+1=${∁}_{6}^{r}{x}^{6-r}(-\frac{1}{x})^{r}$=(-1)r${∁}_{6}^{r}$x6-2r,
令6-2r=2,解得r=2.
∴二项式(x-$\frac{1}{x}$)n展开式中x2的系数为${∁}_{6}^{2}$=15.
故答案为:15.
点评 本题考查了利用导数研究函数的单调性、二项式定理的性质及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知定义在R上的函数f(x)的导函数为f′(x),对任意x∈R满足f(x)+f′(x)<0,则下列结论正确的是( )
| A. | e2f(2)>e3f(3) | B. | e2f(2)<e3f(3) | C. | e2f(2)≥e3f(3) | D. | e2f(2)≤e3f(3) |
2.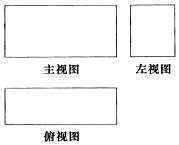 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )| A. | 3$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 6$\sqrt{5}$+4 | D. | 10 |
5.已知a>0,-1<b<0,那么下列不等式成立的是( )
| A. | a<ab<ab2 | B. | ab<a<ab2 | C. | ab<ab2<a | D. | ab2<a<ab |