题目内容
已知S、A、B、C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA＝AB＝1，BC＝
，则球O的表面积等于( )
A．4π B．3π
C．2π D．π
A
[解析]
∵AB⊥BC，∴AC为截面圆的直径，∴AC中点为截面圆的圆心．
设D为AC中点，连OD，则OD⊥平面ABC，
∵SA⊥平面ABC，
∴SA∥OD.
连SC，则SC＝
＝2.
又SB＝，BC＝，∵SC2＝SB2＋BC2，
∴∠SBC＝90°，∵∠SAC＝90°，∴SC为球O的直径，
∵2R＝2，故R＝1，∴S球＝4πR2＝4π，选A.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
＝
，则三棱锥与球的体积之比为________．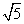
]
]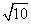