题目内容
1.已知等比数列{an}满足a4a5a6=8,a2=1,则a2+a5+a8+a11=( )| A. | 7 | B. | 15 | C. | 16 | D. | 53 |
分析 由题意,a5=2,a2=1,q3=2,a2+a5+a8+a11=3+a2q6+a2q9,即可得出结论.
解答 解:由题意,a5=2,a2=1,q3=2,
∴a2+a5+a8+a11=3+a2q6+a2q9=3+4+8=15,
故选B.
点评 本题考查了等比数列的通项公式,考查了等比数列的性质,是基础的计算题.

练习册系列答案
相关题目
4.函数f(x)是定义在R上的奇函数,对任意两个不相等的正数x1,x2,都有$\frac{{x}_{2}f({x}_{1})-{x}_{1}f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,记a=-log23•f(log${\;}_{\frac{1}{3}}$2),b=f(1),c=4f(0.52),则( )
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<b<c |
9.设函数f(x)在(-∞,+∞)上有意义,对于对定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}{f(x),f(x)<k}\\{k,f(x)≥k}\end{array}\right.$取k=$\frac{1}{2}$,f(x)=($\frac{1}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
13.已知函数f(x)=Asin(ωx+φ)+B,(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,则( )
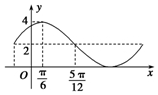

| A. | A=4 | B. | ω=1 | C. | φ=$\frac{π}{6}$ | D. | B=4 |
10.空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现处足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2016年8月某日某省x个监测点数据统计如下:
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)在空气污染指数分别为50~100和150~200的监测点中,用分层抽样的方法抽取10个监测点,从中任意选取4个监测点,求这4个监测点中空气质量为良的个数ξ的期望.
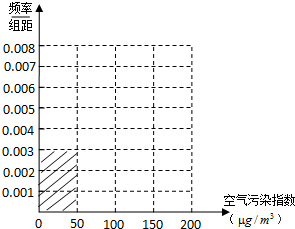
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
(Ⅱ)在空气污染指数分别为50~100和150~200的监测点中,用分层抽样的方法抽取10个监测点,从中任意选取4个监测点,求这4个监测点中空气质量为良的个数ξ的期望.

11.若sinα>0且tanα<0,则$\frac{α}{2}$的终边在( )
| A. | 第一象限 | B. | 第二象限 | ||
| C. | 第一象限或第三象限 | D. | 第三象限或第四象限 |
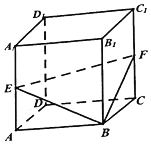 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].