题目内容
已知向量
=(1,2),
=(x,4),且
∥
,则实数x= .
| a |
| b |
| a |
| b |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:直接由向量共线的坐标表示列式计算x的值.
解答:
解:由向量
=(1,2),
=(x,4),
∵
∥
,
∴1×4-2x=0,
解得:x=2.
故答案为:2.
| a |
| b |
∵
| a |
| b |
∴1×4-2x=0,
解得:x=2.
故答案为:2.
点评:共线问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0.是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
下列函数中,在区间(0,2)上是增函数的是( )
| A、y=x2-4x+5 | ||
B、y=
| ||
| C、y=2-x | ||
D、y=log
|
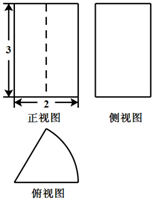 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )A、
| ||
B、
| ||
| C、π | ||
| D、2π |