题目内容
7.已知焦距为2$\sqrt{3}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1、上顶点为D,直线DF1与椭圆C的另一个交点为H,且|DF1|=7|F1H|.求椭圆的方程.分析 设|DF1|=7|F1H|=7m.D,F1到准线的距离为$\frac{7m}{e}$,$\frac{m}{e}$.利用直线的斜率,即可求出椭圆的方程.
解答 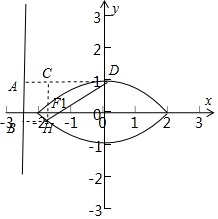 解:设|DF1|=7|F1H|=7m.D,F1到准线的距离为$\frac{7m}{e}$,$\frac{m}{e}$.
解:设|DF1|=7|F1H|=7m.D,F1到准线的距离为$\frac{7m}{e}$,$\frac{m}{e}$.
设直线DF1的倾斜角为α,则cosα=$\frac{3}{4e}$.
∵tanα=$\frac{b}{c}$,∴cosα=$\frac{c}{a}$,
∴$\frac{c}{a}$=$\frac{3}{4e}$,
∵c=$\sqrt{3}$,∴a=2.∴b=1,
∴椭圆的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
点评 本题考查椭圆的方程与性质,考查椭圆的定义,属于中档题.

练习册系列答案
相关题目
15.已知等比数列{an}的前n项和为Sn,若S3=7,S6=63,则数列{nan}的前n项和为( )
| A. | -3+(n+1)×2n | B. | 3+(n+1)×2n | C. | 1+(n+1)×2n | D. | 1+(n-1)×2n |
12.总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
| 7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 1128 | 0598 |
| 3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
| A. | 11 | B. | 02 | C. | 05 | D. | 04 |
19.已知f(x)是定义在实数集R上的不恒为零的偶函数,且xf(x+1)=(x+1)f(x)对任意实数x恒成立,则$f[f(\frac{5}{2})]$的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
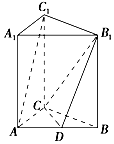 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.