��Ŀ����
19����ֱ������ϵxOy�У�������ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ��������C��������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������ֱ��l�ļ����귽��Ϊ��cos����-$\frac{��}{4}$��=2$\sqrt{2}$����1��д������C����ͨ���̺�ֱ��l��ֱ�����귽�̣�
��2��������C�ϵĵ㵽ֱ��l�ľ�������ֵ��
���� ��1������C����������ȥ�����ȣ����������C�ķ��̣��ɦ�cos��=x����sin��=y�������ֱ��l��ֱ�����귽�̣�
��2��������C�ϵĵ�Ϊ��$\sqrt{3}cos��$��sin�ȣ������õ㵽ֱ�ߵľ��빫ʽ���������C�ϵĵ㵽ֱ��l�ľ�������ֵ��
��� �⣺��1������C��������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
��ȥ�����ȣ�������C�ķ���Ϊ$\frac{x^2}{3}+{y^2}=1$��
ֱ��l�ļ����귽��Ϊ��cos����-$\frac{��}{4}$��=2$\sqrt{2}$��
��$�ѣ�cos��cos\frac{��}{4}+sin��sin\frac{��}{4}��$=2$\sqrt{2}$��
�������æ�cos��+��sin��=4��
�ߦ�cos��=x����sin��=y��
ֱ��l��ֱ�����귽��Ϊx+y-4=0��
��2��������C�ϵĵ�Ϊ��$\sqrt{3}cos��$��sin�ȣ���
������C�ϵĵ㵽ֱ��l�ľ��룺
$d=\frac{{|{\sqrt{3}cos��+sin��-4}|}}{{\sqrt{2}}}=\frac{{|{2sin����+\frac{��}{3}��-4}|}}{{\sqrt{2}}}��3\sqrt{2}$��
������C�ϵĵ㵽ֱ��l�ľ�������ֵ${d_{max}}=3\sqrt{2}$��
���� ���⿼�����ߵ���ͨ���̺�ֱ�ߵ�ֱ�����귽�̵������������ϵĵ㵽ֱ��l�ľ�������ֵ�������鼫���ꡢֱ������Ļ���������������֤�����������������������ת������˼�롢���ν��˼�룬���е��⣮

| A�� | ��С������Ϊ�е��溯�� | B�� | ��С������Ϊ�е�ż���� | ||
| C�� | ��С������Ϊ$\frac{��}{2}$���溯�� | D�� | ��С������Ϊ$\frac{��}{2}$��ż���� |
| A�� | 3x-y-5=0 | B�� | x-3y+9=0 | C�� | 3x+y-13=0 | D�� | x+3y-15=0 |

�����г�����������ж���ȷ���ǣ�������
| A�� | $S=\frac{100}{101}��P=\frac{100}{101}$ | B�� | $S=\frac{99}{100}��P=\frac{99}{202}$ | ||
| C�� | $S=\frac{100}{101}��P=\frac{99}{202}$ | D�� | $S=\frac{100}{101}��P=\frac{99}{100}$ |
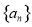 ����ǰn���Ϊ
����ǰn���Ϊ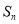 ����
���� �ɵȲ����У�������
�ɵȲ����У�������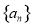 ��ͨ�ʽΪ�� ��
��ͨ�ʽΪ�� ��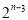 B��
B��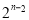 C��
C��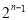 D��
D��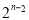 +1
+1